Teraz matura. Klasa 4. Zbiór zadań. Poziom podstawowy – rozwiązania i odpowiedzi

Zbiór zadań, Wydawnictwo: Nowa Era

Zadanie 8, b) - strona 36

W tym zadaniu wyznacz odpowiedni wzór funkcyjny i zapisać go w postaci kanonicznej i iloczynowej, jeżeli punkty A i B należą do wykresu paraboli.
$\text{[math]}$

Punkt B to miejsce przecięcia się z osią OY $\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

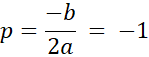
Z symetrii paraboli:

$\text{[math]}$

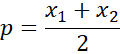
Z punktu A wynika $\text{[math]}$

Zatem $\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Z punktu B wynika współczynnik c, ponieważ jest to miejsce przecięcia się paraboli z osią OY. Mając c, korzystając z punktu A, który przedstawia miejsce zerowe funkcji, wyliczamy współczynnik b, podstawiając wartości punktu jako argument i wartość funkcji. Otrzymujemy wzór ogólny i definiujemy wierzchołek paraboli definicyjnymi wzorami. Aby wyznaczyć drugie miejsce zerowe, korzystamy z faktu, że współrzędna p wierzchołka paraboli jest średnią symetryczną miejsc zerowych.

Zadanie 7, strona 164, Matematyka. Klasa 2. Podręcznik. Zakres rozszerzony – rozwiązania i odpowiedzi

Zadanie 8, strona 224, Matematyka. Klasa 6. Podręcznik - rozwiązania i odpowiedzi

Zadanie 5., strona 9, Matematyka z plusem. Klasa 6. Zeszyt ćwiczeń - rozwiązania i odpowiedzi

Zadanie 15., strona 77, Matematyka wokół nas. Klasa 8. Podręcznik - rozwiązania i odpowiedzi

Zadanie 3, strona 211, Matematyka. Klasa 1. Podręcznik. Zakres rozszerzony. Część 1 – rozwiązania i odpowiedzi

Zadanie 20, strona 255, MATeMAtyka. Klasa 3. Zbiór zadań. Zakres podstawowy i rozszerzony – rozwiązania i odpowiedzi

Zadanie 27, strona 138, Teraz matura. Klasa 4. Zbiór zadań. Poziom podstawowy – rozwiązania i odpowiedzi

Zadanie 1., strona 36, Matematyka. Klasa 1. Zakres podstawowy. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 4., strona 95, Matematyka. Klasa 7. Zeszyt ćwiczeń - rozwiązania i odpowiedzi

Zadanie 9.13., strona 265, Matematyka. Prosto do matury. Klasa 1. Zakres podstawowy i rozszerzony. Podręcznik - rozwiązania i odpowiedzi

Zadanie 1

36

36

36

36

Zadanie 2

36

36

36

36

Zadanie 3

36

36

36

36

Zadanie 4

36

36

36

36

Zadanie 5

36

36

36

36

36

Zadanie 6

36

36

36

36

36

Zadanie 7

36

36

36

36

Zadanie 8

36

36

36

36

Zadanie 9

37

37

37

Zadanie 10

37

37

37

37

Zadanie 12

37

37

37

37

37

Zadanie 13

37

37

37

37

37

Zadanie 15

37

37

37

37

37

Zadanie 16

37

37

37

37

Zadanie 17

37

37

37

37

37

37

37

Zadanie 18

38

38

38

38

Zadanie 19

38

38

38

38

Zadanie 20

38

38

38

38

Zadanie 21

38

38

38

38

Zadanie 22

38

38

38

38

38

Zadanie 23

38

38

38

38

Zadanie 24

38

38

38

38

38

38

38

38

38

38

38

38

Zadanie 30

39

39

39

39

39

Zadanie 31

39

39

39

39

39

39

39

39

39

39

39

Zadanie 38

39

39

39

39

40

40

40

40

40

40

40

40

41

41

41

41

41

41

41

41

42

42

42

42

42

42

42

42

42

42

42

42

43

43

43

43

43

43

43

43

43

44

Zadanie 2

44

44

44

44

44

44

44

44

44

44

Pełny spis treści