W tym zadaniu należy podać miejsca przecięcia się funkcji z osiami układu współrzędnych oraz jej postać kanoniczną i iloczynową, a także naszkicować jej wykres.
Lub
brak przecięcia
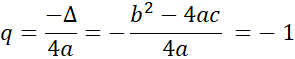
Postać iloczynowa: nie istnieje
Postać kanoniczna:
Wykres:
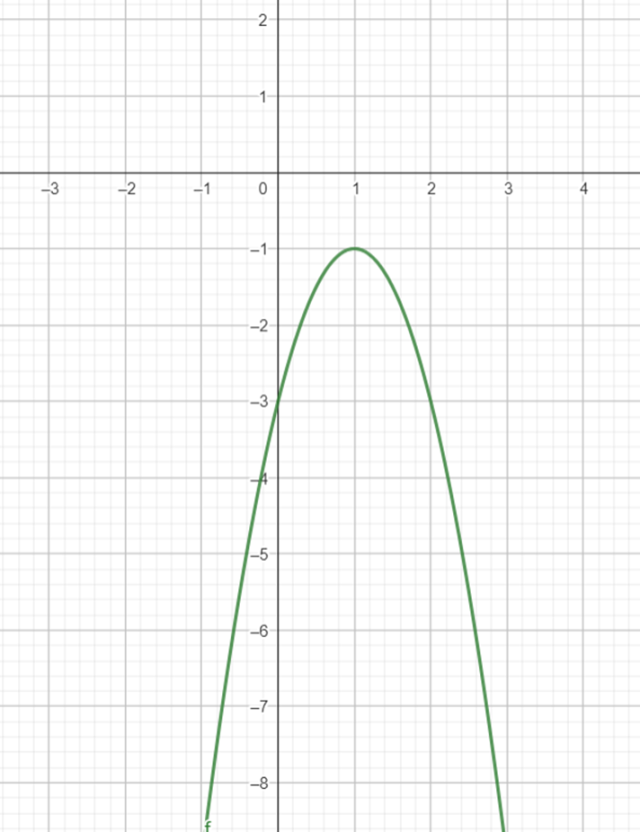
Miejsce przecięcia się z osią OY to wartość funkcji w zerze, natomiast miejsca przecięcia się funkcji z osią OX, to argumenty, dla których funkcja ma wartość zero – inaczej mówiąc, miejsca zerowe tej funkcji. W naszym przypadku wyróżnik trójmianu kwadratowego (delta) jest ujemny, zatem miejsca zerowe tej funkcji nie istnieją, współczynnik a jest ujemny, zatem znajduje się ona w całości pod osią OX.
Dodatkowo liczymy współrzędne wierzchołka naszej paraboli (p, q) korzystając ze wzorów:
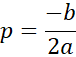
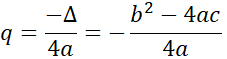
Otrzymane wartości używamy do skonstruowania postaci kanonicznej danej przepisem funkcyjnym:
