Teraz matura. Klasa 4. Zbiór zadań. Poziom podstawowy – rozwiązania i odpowiedzi

Zbiór zadań, Wydawnictwo: Nowa Era

Zadanie 13 - strona 43

W tym zadaniu wyznacz wzór funkcji paraboli, która przyjmuje najmniejszą wartość równą $\text{[math]}$ dla x = 2, a do jej wykresu należy punkt $\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

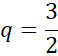
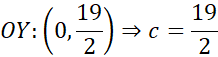
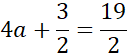
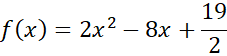
Mając współrzędne wierzchołka paraboli, tworzymy jej postać kanoniczną, w której nieznana jest jedynie a. Rozwijając postać kanoniczną, otrzymujemy postać ogólną, gdzie wyraźne jest, że $\text{[math]}$ . Z informacji o przecięciu wykresu z osią OY, wnioskujemy, że $\text{[math]}$ . Z równania, jakie otrzymujemy, porównując współczynniki c, otrzymujemy współczynnik a i podstawiając go do rozwiniętej postaci kanonicznej, dostajemy postać ogólną funkcji.

Zadanie 8, strona 53, Matematyka wokół nas. Klasa 5. Zeszyt ćwiczeń. Część 1 – rozwiązania i odpowiedzi

Zadanie 3, strona 63, Matematyka z plusem. Klasa 5. Zeszyt Ćwiczeń – rozwiązania i odpowiedzi

Zadanie 17., strona 63, Matematyka. Klasa 2. Zakres podstawowy. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 3, strona 189, Matematyka z plusem. Klasa 8. Podręcznik – rozwiązania i odpowiedzi

Zadanie 8.25., strona 200, Matematyka. Klasa 3. Zbiór zadań. Zakres rozszerzony – rozwiązania i odpowiedzi

Zadanie 21, strona 41, MATeMAtyka. Klasa 3. Zbiór zadań. Zakres podstawowy i rozszerzony – rozwiązania i odpowiedzi

Ćwiczenie 26., strona 33, Matematyka i przykłady jej zastosowań. Klasa 1. Podręcznik. Zakres podstawowy – rozwiązania i odpowiedzi

Zadanie 14, strona 39, Przygotowanie do egzaminu ósmoklasisty. Klasa 7. Zestawy zadań. Matematyka - rozwiązania i odpowiedzi

Zadanie 87., strona 201, Matematyka z plusem. Klasa 2. Zbiór zadań. Zakres podstawowy i rozszerzony – rozwiązania i odpowiedzi

Zadanie 4., strona 52, Matematyka z plusem. Klasa 5. Podręcznik - rozwiązania i odpowiedzi

Zadanie 1

36

36

36

36

Zadanie 2

36

36

36

36

Zadanie 3

36

36

36

36

Zadanie 4

36

36

36

36

Zadanie 5

36

36

36

36

36

Zadanie 6

36

36

36

36

36

Zadanie 7

36

36

36

36

Zadanie 8

36

36

36

36

Zadanie 9

37

37

37

Zadanie 10

37

37

37

37

Zadanie 12

37

37

37

37

37

Zadanie 13

37

37

37

37

37

Zadanie 15

37

37

37

37

37

Zadanie 16

37

37

37

37

Zadanie 17

37

37

37

37

37

37

37

Zadanie 18

38

38

38

38

Zadanie 19

38

38

38

38

Zadanie 20

38

38

38

38

Zadanie 21

38

38

38

38

Zadanie 22

38

38

38

38

38

Zadanie 23

38

38

38

38

Zadanie 24

38

38

38

38

38

38

38

38

38

38

38

38

Zadanie 30

39

39

39

39

39

Zadanie 31

39

39

39

39

39

39

39

39

39

39

39

Zadanie 38

39

39

39

39

40

40

40

40

40

40

40

40

41

41

41

41

41

41

41

41

42

42

42

42

42

42

42

42

42

42

42

42

43

43

43

43

43

43

43

43

43

44

Zadanie 2

44

44

44

44

44

44

44

44

44

44

Pełny spis treści