Teraz matura. Klasa 4. Zbiór zadań. Poziom podstawowy – rozwiązania i odpowiedzi

Zbiór zadań, Wydawnictwo: Nowa Era

Zadanie 8, c) - strona 36

W tym zadaniu wyznacz odpowiedni wzór funkcyjny i zapisać go w postaci kanonicznej i iloczynowej, jeżeli punkty A i B należą do wykresu paraboli.
$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

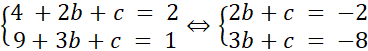
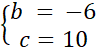
$\text{[math]}$ brak miejsc zerowych

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

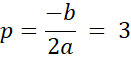
Podstawiamy współrzędne punktów pod wzór funkcji i tworzymy układ równań, z którego wyliczamy współczynniki b i c, dzięki czemu otrzymujemy ogólny wzór funkcji. Licząc wyróżnik trójmianu kwadratowego, okazuje się, że jest on ujemny, zatem postać iloczynowa nie istnieje (ponieważ rzeczywiste miejsca zerowe nie istnieją). Korzystając z definicyjnych wzorów, wyznaczamy współrzędne wierzchołka paraboli i tworzymy wzór funkcji w postaci kanonicznej.

Zadanie 8, strona 107, Matematyka z kluczem. Klasa 5. Podręcznik. Część 2 – rozwiązania i odpowiedzi

Zadanie 5., strona 234, Matematyka wokół nas. Klasa 8. Podręcznik - rozwiązania i odpowiedzi

Zadanie 20., strona 84, Matematyka. Klasa 8. Podręcznik - rozwiązania i odpowiedzi

Ćwiczenie F, strona 168, Matematyka z plusem. Klasa 4. Podręcznik - rozwiązania i odpowiedzi

Zadanie 11.17, strona 262, Matematyka i przykłady jej zastosowań. Klasa 1.Podręcznik. Zakres podstawowy i rozszerzony - rozwiązania i odpowiedzi

Ćwiczenie 9, strona 91, Matematyka z kluczem. Klasa 5. Zeszyt ćwiczeń - rozwiązania i odpowiedzi

Zadanie 3, strona 52, Matematyka wokół nas. Klasa 7. Zeszyt ćwiczeń – rozwiązania i odpowiedzi

Zadanie 1, strona 148, Matematyka. Klasa 7. Podręcznik – rozwiązania i odpowiedzi

Zadanie 11, strona 112, Matematyka. Klasa 5. Podręcznik. Część 1 - rozwiązania i odpowiedzi

Zadanie 17., strona 40, Matematyka z kluczem. Klasa 8. Zbiór zadań – rozwiązania i odpowiedzi

Zadanie 1

36

36

36

36

Zadanie 2

36

36

36

36

Zadanie 3

36

36

36

36

Zadanie 4

36

36

36

36

Zadanie 5

36

36

36

36

36

Zadanie 6

36

36

36

36

36

Zadanie 7

36

36

36

36

Zadanie 8

36

36

36

36

Zadanie 9

37

37

37

Zadanie 10

37

37

37

37

Zadanie 12

37

37

37

37

37

Zadanie 13

37

37

37

37

37

Zadanie 15

37

37

37

37

37

Zadanie 16

37

37

37

37

Zadanie 17

37

37

37

37

37

37

37

Zadanie 18

38

38

38

38

Zadanie 19

38

38

38

38

Zadanie 20

38

38

38

38

Zadanie 21

38

38

38

38

Zadanie 22

38

38

38

38

38

Zadanie 23

38

38

38

38

Zadanie 24

38

38

38

38

38

38

38

38

38

38

38

38

Zadanie 30

39

39

39

39

39

Zadanie 31

39

39

39

39

39

39

39

39

39

39

39

Zadanie 38

39

39

39

39

40

40

40

40

40

40

40

40

41

41

41

41

41

41

41

41

42

42

42

42

42

42

42

42

42

42

42

42

43

43

43

43

43

43

43

43

43

44

Zadanie 2

44

44

44

44

44

44

44

44

44

44

Pełny spis treści