![]()
Gdzie:
![]() - czynnik Lorentza
- czynnik Lorentza

![]() - masa cząstki
- masa cząstki
![]() - prędkość światła
- prędkość światła
![]() - energia spoczynkową cząsteczki
- energia spoczynkową cząsteczki
Z podanych równań wiemy, że:

Podstawiając wzór na Ek:

Otrzymujemy:


Podstawiając do wzoru :
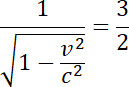




Jeśli prędkość światła wynosi
![]() , to szybkość cząstki wynosi:
, to szybkość cząstki wynosi:

![]()
![]()
![]()

Zadanie polega na znalezieniu prędkości cząstki, korzystając z relacji między jej energią kinetyczną, energią spoczynkową oraz czynnikiem Lorentza. Na początek należy określić, że energia kinetyczna cząstki jest dwukrotnie większa od jej energii spoczynkowej.
Następnie, przy użyciu czynnika Lorentza, który opisuje, jak obiekty zachowują się w relatywistycznych prędkościach w porównaniu do prędkości światła, możesz przekształcić tę informację, by znaleźć stosunek prędkości cząstki do prędkości światła.
Po rozwiązaniu równań dostajesz, że cząstka porusza się z prędkością, która stanowi pewien ułamek prędkości światła. Aby uzyskać dokładną wartość, musisz pomnożyć ten ułamek przez znane nam prędkości światła, czyli 300,000 km/s, co da Ci końcowy wynik prędkości cząstki.