Poprawna jest odpowiedź A. Pasażerowie A i B na platformie złapią piłki w tym samym czasie niezależnie od tego, czy obserwujemy ich z perspektywy podłoża, czy z perspektywy samej platformy.
Ruch piłki skierowanej ku pasażerowi B opisuje równanie:
![]()
Tymczasem ruch pasażera B jest opisany przez:
![]()
Kiedy obie wartości będą takie same, oznacza to, że piłka dotarła do pasażera B:
![]()
![]() - czas ruchu piłki 1
- czas ruchu piłki 1
Podobnie, ruch piłki skierowanej ku pasażerowi A można opisać jako:
![]() , natomiast położenie pasażera A to
, natomiast położenie pasażera A to
![]()
Kiedy te dwie wartości się spotkają:
![]()
![]() - czas ruchu piłki 2
- czas ruchu piłki 2
Według obserwatora na podłożu (obserwator C) obie piłki zostaną złapane w tym samym czasie przez pasażerów A i B.
Ruch piłki w kierunku B jest opisany przez:
![]() . W tym układzie B jest nieruchomy, więc
. W tym układzie B jest nieruchomy, więc
![]() .
.
Stąd:
![]()
Dla piłki w kierunku A mamy:
![]() , natomiast A jest w odległości
, natomiast A jest w odległości
![]() od punktu początkowego.
od punktu początkowego.
Równanie dla piłki w kierunku A daje nam:
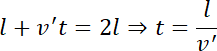
Obserwując z platformy, obaj pasażerowie złapią piłki równocześnie.
Podsumowując, niezależnie od wybranego układu odniesienia, obie piłki będą poruszać się tyle samo czasu, zanim zostaną złapane przez odpowiednich pasażerów.

W układzie odniesienia związanego z podłożem (obserwator C) obserwujemy zarówno ruch platformy, jak i piłek wyrzuconych w lewo i w prawo. Kiedy człowiek na platformie wyrzuca piłki z pewną prędkością względem platformy, piłki będą miały tę prędkość zsumowaną z prędkością platformy (w przypadku piłki wyrzuconej w kierunku ruchu platformy) lub odjętą od prędkości platformy (w przypadku piłki wyrzuconej w przeciwnym kierunku). Z matematycznego modelowania wynika, że obie piłki dotrą do pasażerów A i B w tym samym czasie.
W tym układzie odniesienia związanego z platformą (obserwator na platformie) platforma jest nieruchoma, więc widzimy jedynie ruch piłek. Człowiek wyrzucający piłki dostrzega je poruszające się z tą samą prędkością, ale w przeciwnych kierunkach. Z matematycznej analizy wynika, że obie piłki dotrą do pasażerów A i B jednocześnie, co jest zgodne z intuicją - w końcu piłki zostały wyrzucone równocześnie z tego samego miejsca i z tą samą prędkością.
Główną ideą stojącą za tym rozwiązaniem jest to, że prędkość wyrzutu piłki względem platformy jest stała. W obu układach odniesienia, różnica w obserwowanych prędkościach wynika z prędkości platformy względem podłoża. Matematyczne modelowanie ruchu pozwoli Ci przewidzieć, że w obu układach odniesienia piłki dotrą do pasażerów jednocześnie.