Twoim zadaniem jest wyprowadzenie wzoru na energię kinetyczną cząstki oraz obliczenie jej wartości. Po odliczeniu wartości wynik podaj w megadektronowoltach.

$\text{[math]}$

Energia całkowita cząstki to suma jej energii kinetycznej i spoczynkowej:

$\text{[math]}$

Zatem kwadrat energii całkowitej:

$\text{[math]}$

Relacja pomiędzy energią całkowitą cząstki, pędem i jej masą:

$\text{[math]}$

Przyrównujemy oba wzory na energię całkowitą:

$\text{[math]}$

Upraszczamy:

$\text{[math]}$

Uzyskaliśmy równanie kwadratowe o postaci: $\text{[math]}$ , gdzie: $\text{[math]}$ , $\text{[math]}$ , $\text{[math]}$ oraz $\text{[math]}$

$\text{[math]}$

Podstawmy odpowiednie dane:

$\text{[math]}$ | $\text{[math]}$

$\text{[math]}$

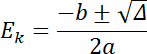
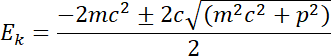
Energia kinetyczna musi mieć wartość dodatnią, więc:

$\text{[math]}$

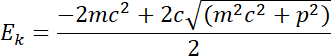
Uprośćmy wzór:

$\text{[math]}$

Podstawmy zatem odpowiednie dane, pamiętając, że $\text{[math]}$ $\text{[math]}$ :

$\text{[math]}$

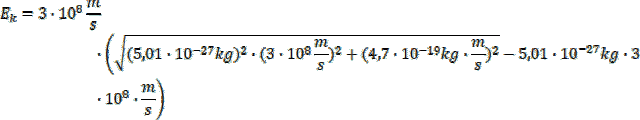
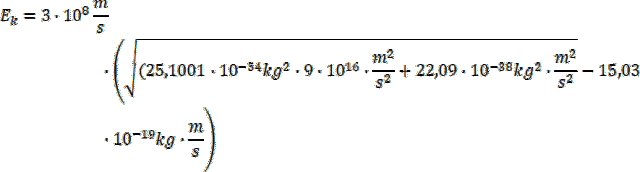
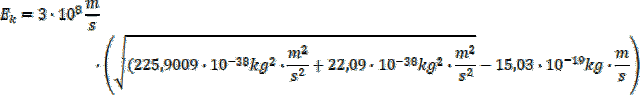
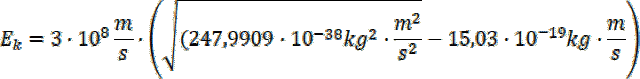
Konwertując jednostki energii z jouli ( $\text{[math]}$ ) na elektronowolty ( $\text{[math]}$ ):

$\text{[math]}$

W zadaniu chcemy znaleźć energię kinetyczną $\text{[math]}$ cząstki, mając dane jej masę, pęd oraz prędkość światła. Do tego celu wykorzystaj dwie kluczowe relacje z fizyki relatywistycznej:

1. Relacja między energią całkowitą cząstki, jej pędem i masą. Energię całkowitą możemy traktować jako sumę energii kinetycznej cząstki i energii odpowiadającej jej masie spoczynkowej (czyli energii związanej z samą obecnością cząstki w przestrzeni, niezależnie od jej ruchu).

2. Wzór, który opisuje energię całkowitą cząstki jako sumę jej energii kinetycznej i energii spoczynkowej.

Kombinując te dwie relacje, otrzymujemy równanie kwadratowe dla energii kinetycznej. Następnie obliczamy dyskryminant tego równania i wykorzystujemy go do rozwiązania równania i znalezienia energii kinetycznej. Końcowy wynik przedstawiamy w jednostkach MeV (megaelektronowolty).