Podaj obwód czworokąta, którego stosunek długości boków jest równy 8 : 7 : 5 : 2, a różnica między najdłuższym i najkrótszym wynosi 3 cm.
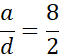
a – d = 3 cm
2a = 8d / : 2
a = 4d
4d – d = 3
3d = 3 / : 3
d = 1 cm
a = 4 · 1 cm
a = 4 cm
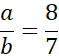
8b = 7a
8b = 28 / : 8
b = 3,5 cm
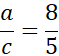
8c = 5a
8c = 20 /: 8
c = 2,5 cm
Obw. = a + b + c + d = 4 cm + 3,5 cm + 2,5 cm + 1 cm = 11 cm
Odp.: Obwód tego czworokąta wynosi 11 cm.

Musisz utworzyć odpowiednie proporcje, skorzystaj również z informacji o najdłuższym i najkrótszym boku, a następnie rozwiąż układ równań. Pamiętaj, że proporcje możesz obliczać tzw. sposobem na krzyż:
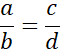
ad = bc

Zadanie 1.
70Zadanie 2.
71Zadanie 3.
71Zadanie 4.
71Zadanie 6.
72Zadanie 8.
72Zadanie 1.
74Zadanie 2.
75Zadanie 5.
75Zadanie 6.
75Zadanie 10.
76Zadanie 12.
77Zadanie 2.
80Zadanie 3.
80Zadanie 4.
80Zadanie 7.
80Zadanie 8.
80Zadanie 9.
80Zadanie 10.
80Zadanie 12.
81Zadanie 13.
81Zadanie 14.
81Zadanie 15.
81Zadanie 17.
81Zadanie 18.
82Zadanie 19.
82Zadanie 20.
82Zadanie 21.
82Zadanie 4.
85Zadanie 20.
88Zadanie 21.
88Zadanie 22.
88Ćwiczenie 5.
92Ćwiczenie 9.
92Ćwiczenie 10.
92
