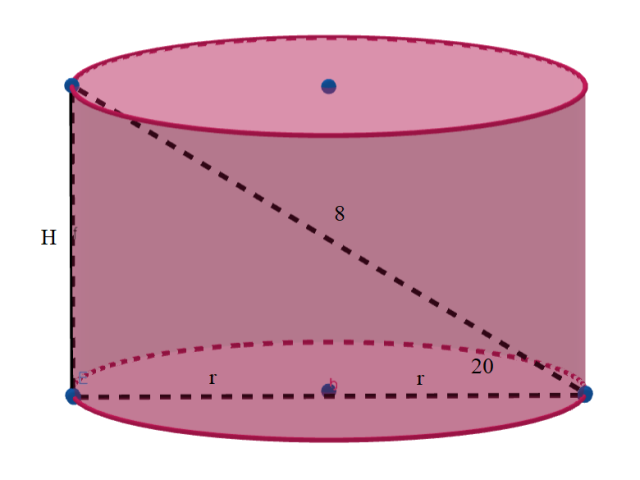
W tym zadaniu oblicz objętość i pole powierzchni danego walca wiedząc, że kąt między przekątną przekroju osiowego a średnicą jego podstawy ma miarę 20°. Przekątna ma długość 8.
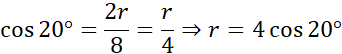
r = 4 ∙ 0,9397 = 3,7588
2r = 2 ∙ 3,7588 = 7,5176
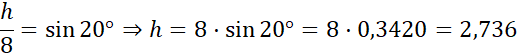
![]()
![]()

Wyznacz promień podstawy korzystając z funkcji cosinus. Cosinusem kąta α nazywamy stosunek długości przyprostokątnej leżącej przy kącie α do długości przeciwprostokątnej.
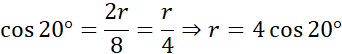
Odczytaj wartość kąta z tabeli na stronie 249.
r = 4 ∙ 0,9397 = 3,7588
2r = 2 ∙ 3,7588 = 7,5176
Wyznacz wysokość H. Skorzystaj z funkcji sinus. Sinusem kąta α nazywamy stosunek długości przyprostokątnej leżącej naprzeciw kąta α do długości przeciwprostokątnej.
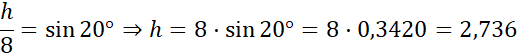
Objętość walca wyznacza się ze wzoru ![]()
![]()
Pole powierzchni całkowitej walca wyznacza się ze wzoru ![]()
![]()

Zadanie 2
218Zadanie 3
218Zadanie 4
218Zadanie 5
218Zadanie 6
218Zadanie 7
219Zadanie 8
219Zadanie 9
219Zadanie 10
219Zadanie 13
219Zadanie 14
220Zadanie 15
220Zadanie 17
220Zadanie 18
220Zadanie 24
221Zadanie 25
221Zadanie 26
222Zadanie 27
222Zadanie 2
227Zadanie 4
228Zadanie 5
228Zadanie 6
228Zadanie 7
228Zadanie 8
228Zadanie 9
228Zadanie 10
229Zadanie 11
229Zadanie 13
229Zadanie 14
229Zadanie 15
229Zadanie 16
230Zadanie 2
233Zadanie 3
233Zadanie 4
234Zadanie 6
234Zadanie 14
235Zadanie 1
240Zadanie 2
240Zadanie 9
241Zadanie 11
241Zadanie 16
242Zadanie 1
245Zadanie 4
246Zadanie 5
246Zadanie 7
246Zadanie 9
246Zadanie 12
247
