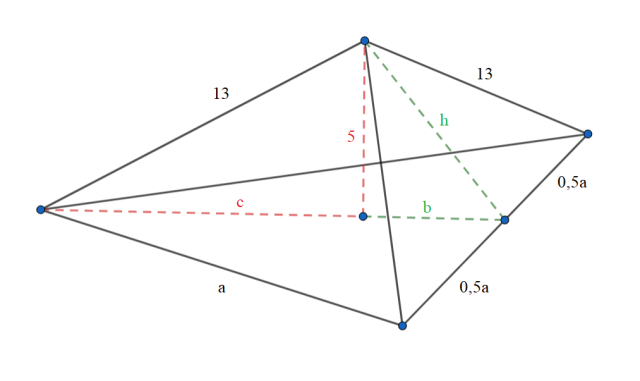
W tym zadaniu oblicz odległość spodka wysokości ostrosłupa od krawędzi bocznej, jeśli jest to ostrosłup prawidłowy czworokątny, krawędź jego podstawy wynosi 4, a krawędź boczna 6.
c2 + 52 = 132
c2 + 25 = 169 / - 25
c2 =144
c = 12
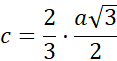
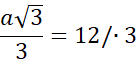
![]()
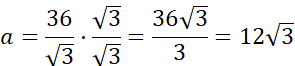
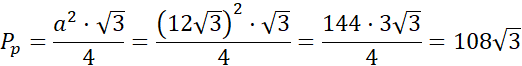
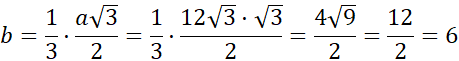
h2 = 62 + 52
h2 = 36 + 25
h2 = 61
![]()
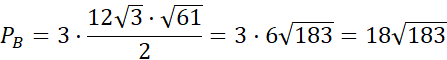
![]()
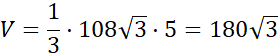

Wyznacz długość c. Skorzystaj z twierdzenia Pitagorasa a2 + b2 = c2, gdzie a i b to długości przyprostokątnych, a c to przeciwprostokątna trójkąta prostokątnego.
c2 + 52 = 132
c2 + 25 = 169 / - 25
c2 =144
c = 12
Skorzystaj z własności, że c to dwie trzecie wysokości trójkąta równobocznego.
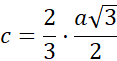
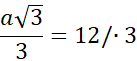
![]()

Wyznacz pole podstawy ostrosłupa.
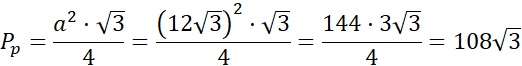
Skorzystaj z własności, że b to jedna trzecia wysokości trójkąta równobocznego.
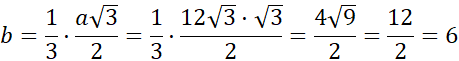
Wyznacz wysokość ściany bocznej h korzystając z twierdzenia Pitagorasa.
h2 = 62 + 52
h2 = 36 + 25
h2 = 61
![]()
Wyznacz pole ścian bocznych.
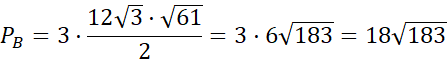
Pole ostrosłupa oblicza się ze wzoru P = Pp + Pb, gdzie Pp to pole podstawy, a Pb to pole wszystkich ścian bocznych.
![]()
Objętość ostrosłupa wyznacza się ze wzoru ![]()
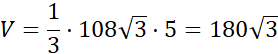

Zadanie 2
218Zadanie 3
218Zadanie 4
218Zadanie 5
218Zadanie 6
218Zadanie 7
219Zadanie 8
219Zadanie 9
219Zadanie 10
219Zadanie 13
219Zadanie 14
220Zadanie 15
220Zadanie 17
220Zadanie 18
220Zadanie 24
221Zadanie 25
221Zadanie 26
222Zadanie 27
222Zadanie 2
227Zadanie 4
228Zadanie 5
228Zadanie 6
228Zadanie 7
228Zadanie 8
228Zadanie 9
228Zadanie 10
229Zadanie 11
229Zadanie 13
229Zadanie 14
229Zadanie 15
229Zadanie 16
230Zadanie 2
233Zadanie 3
233Zadanie 4
234Zadanie 6
234Zadanie 14
235Zadanie 1
240Zadanie 2
240Zadanie 9
241Zadanie 11
241Zadanie 16
242Zadanie 1
245Zadanie 4
246Zadanie 5
246Zadanie 7
246Zadanie 9
246Zadanie 12
247
