W tym zadaniu przyjrzyj się rysunkowi i określ, który z zaznaczonych przekrojów kuli ma większe pole powierzchni i o ile jest ono większe przyjmując, że r = 13 cm, d = 5 cm, α = 120°.
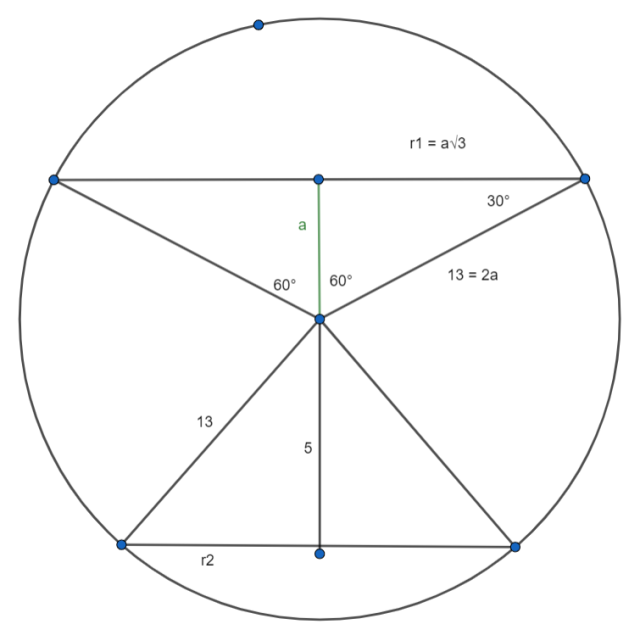
13 = 2a / : 2
a = 6,5
![]()
![]()
52 + r22 = 132
r22 + 25 = 169 / - 25
r22 = 144
r2 = 12
![]()
![]()
Dolny przekrój jest większy o ![]()

Aby obliczyć promień r1, skorzystaj z własności trójkąta o kątach 30˚, 60˚ i 90˚.
13 = 2a / : 2
a = 6,5
![]()
Wzór na pole koła to ![]()
![]()
Wyznacz promień r2. Skorzystaj z twierdzenia Pitagorasa a2 + b2 = c2, gdzie a i b to długości przyprostokątnych, a c to przeciwprostokątna trójkąta prostokątnego.
52 + r22 = 132
r22 + 25 = 169 / - 25
r22 = 144
r2 = 12
![]()
Dolny przekrój ma większe pole. Oblicz różnicę pól.
![]()
Dolny przekrój jest większy o ![]()

Zadanie 2
218Zadanie 3
218Zadanie 4
218Zadanie 5
218Zadanie 6
218Zadanie 7
219Zadanie 8
219Zadanie 9
219Zadanie 10
219Zadanie 13
219Zadanie 14
220Zadanie 15
220Zadanie 17
220Zadanie 18
220Zadanie 24
221Zadanie 25
221Zadanie 26
222Zadanie 27
222Zadanie 2
227Zadanie 4
228Zadanie 5
228Zadanie 6
228Zadanie 7
228Zadanie 8
228Zadanie 9
228Zadanie 10
229Zadanie 11
229Zadanie 13
229Zadanie 14
229Zadanie 15
229Zadanie 16
230Zadanie 2
233Zadanie 3
233Zadanie 4
234Zadanie 6
234Zadanie 14
235Zadanie 1
240Zadanie 2
240Zadanie 9
241Zadanie 11
241Zadanie 16
242Zadanie 1
245Zadanie 4
246Zadanie 5
246Zadanie 7
246Zadanie 9
246Zadanie 12
247
