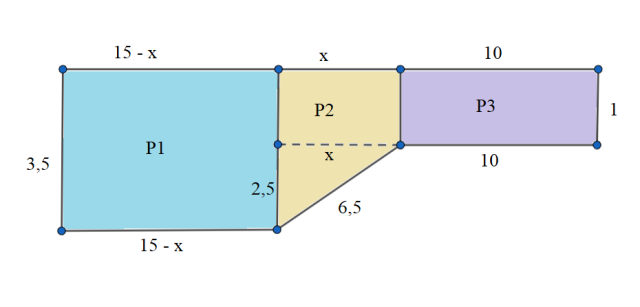
W tym zadaniu oblicz, ile litrów wody potrzeba do napełnienia basenu o kształcie i wymiarach podanych na rysunku.
x2 + 2,52 = 6,52
x2 + 6,25 = 42,25 / - 6,25
x2 = 36
x = 6
P1 = (15 - 6) ∙ 3,5 = 9 ∙ 3,5 = 31,5
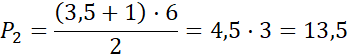
P3 = 10 ∙ 1 = 10
Pp = 31,5 + 13,5 + 10 = 55 m2
H = 12,5m = 125dm
1m2 = 100dm2
55m2 = 5500dm2
V = 5500 ∙ 125 = 687 500 dm3 = 687 500 l
Do basenu zmieści się 687 500 litrów wody.

Podstawa graniastosłupa została zaprezentowana na rysunku. Składa się z 3 figur: 2 prostokątów i trapezu. Oblicz wysokość trapezu x. Skorzystaj z twierdzenia Pitagorasa a2 + b2 = c2, gdzie a i b to długości przyprostokątnych, a c to przeciwprostokątna trójkąta prostokątnego.
x2 + 2,52 = 6,52
x2 + 6,25 = 42,25 / - 6,25
x2 = 36
x = 6
Pole podstawy graniastosłupa to Pp = P1 + P2 + P3.
P1 = (15 - 6) ∙ 3,5 = 9 ∙ 3,5 = 31,5
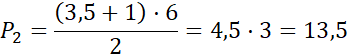
P3 = 10 ∙ 1 = 10
Pp = 31,5 + 13,5 + 10 = 55 m2
Objętość graniastosłupa wyznacza się ze wzoru V = Pp∙ H, gdzie Pp to pole podstawy, a H to wysokość bryły.
Zamień jednostki na decymetry.
H = 12,5m = 125dm
1m2 = 100dm2
55m2 = 5500dm2
V = 5500 ∙ 125 = 687 500 dm3 = 687 500 l
Do basenu zmieści się 687 500 litrów wody.

Zadanie 2
218Zadanie 3
218Zadanie 4
218Zadanie 5
218Zadanie 6
218Zadanie 7
219Zadanie 8
219Zadanie 9
219Zadanie 10
219Zadanie 13
219Zadanie 14
220Zadanie 15
220Zadanie 17
220Zadanie 18
220Zadanie 24
221Zadanie 25
221Zadanie 26
222Zadanie 27
222Zadanie 2
227Zadanie 4
228Zadanie 5
228Zadanie 6
228Zadanie 7
228Zadanie 8
228Zadanie 9
228Zadanie 10
229Zadanie 11
229Zadanie 13
229Zadanie 14
229Zadanie 15
229Zadanie 16
230Zadanie 2
233Zadanie 3
233Zadanie 4
234Zadanie 6
234Zadanie 14
235Zadanie 1
240Zadanie 2
240Zadanie 9
241Zadanie 11
241Zadanie 16
242Zadanie 1
245Zadanie 4
246Zadanie 5
246Zadanie 7
246Zadanie 9
246Zadanie 12
247
