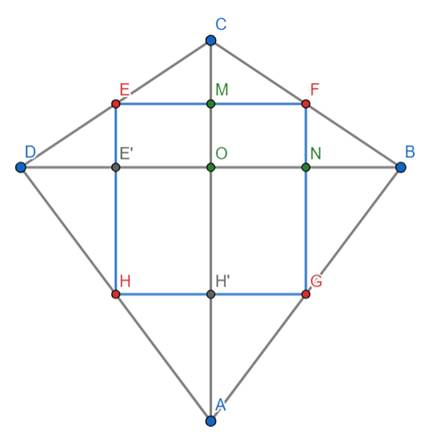
Masz deltoid ABCD w którym:
![]()
Punkty E, F, G, H są środkami boków CD, BC, AB i DA. Wystarczy, że pokażesz:
![]()
Ze względu na symetrię osiową deltoidu dostaniesz wtedy, że pozostałe kąty są proste.
Wiesz, że przekątne deltoidu przecinają się pod kątem prostym:
![]()
W trójkącie BCD, punkty E i F są środkami boków CD oraz BC, czyli:
![]()
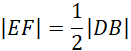
Wynika to z podstawowych proporcji dla trójkątów CEF oraz BCD. Następnie:
![]()
Podobnie pokazujesz, że:
![]()
Z tego wynika, że w czworokącie MFNO:
![]()
![]()
![]()
Z tego wynika, że MFNO jest prostokątem, czyli:
![]()
Dowiodłeś, że czworokąt EFGH jest prostokątem. Zauważ, że:
![]()
![]()
![]()
![]()
Czyli obwód tego prostokąta jest równy sumie długości przekątnych tego deltoidu.

Wykonaj rysunek pomocniczy: