Twoim zadaniem jest uzasadnienie w prosty sposób, że między energią kinetyczną 
Możesz wyrazić związek między energią kinetyczną a potencjalną elektronu, który krąży wokół dowolnej orbity atomu wodoru, za pomocą właściwych równań. Wartość energii potencjalnej elektronu na orbicie n-tej może być obliczona przy użyciu wzoru:
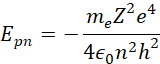
Gdzie:
- 
- 
- 
-
- 
- 
Dla wodoru, który ma liczbę atomową równą 1, energia potencjalna ma uproszczony wzór:
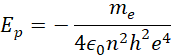
Prędkość elektronu na poszczególnej orbicie można obliczyć wzorem:
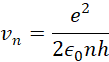
Energię kinetyczną elektronu można przedstawić względem tych danych jako:
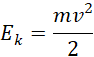
Co prowadzi do wyrażenia:
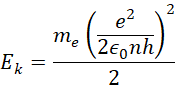
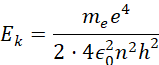
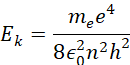
Wówczas zależność między energią potencjalną a energią kinetyczną przyjmuje postać:
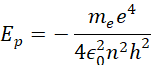
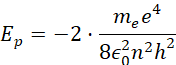
Zależność energii dla satelitów krążących wokół Ziemi można również opisać. Energia potencjalna ciał krążących wokół środka masy, takich jak satelity, jest opisana wzorem:
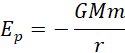
gdzie:
- 
- 
- 
- 
Dla satelitów krążących wokół Ziemi, siła grawitacji pełni rolę siły dośrodkowej i można ją przedstawić jako:
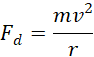
Wartość siły grawitacji przedstaw jako:
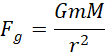
Kwadrat prędkości satelity na dowolnej orbicie będzie miał postać:
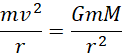
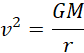
Co prowadzi do wyrażenia energii kinetycznej jako:
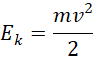
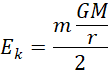
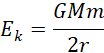
Wówczas zależność między energią potencjalną a energią kinetyczną przyjmuje postać:
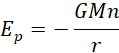
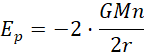
To wyjaśnia zależność między energią potencjalną a kinetyczną dla satelitów krążących wokół Ziemi.
Aby uzasadnić prostym sposobem zależność między energią kinetyczną a potencjalną elektronu na dowolnej orbicie atomu wodoru, musiszzrozumieć, że podobnie jak w przypadku satelitów krążących wokół Ziemi, istnieje siła centralna odpowiedzialna za utrzymanie ruchu obiektu na orbicie. W przypadku atomu wodoru jest to siła elektrostatyczna między naładowanym jądrem a elektronem.
Ta siła centralna jest niezbędna, aby elektron pozostawał na swojej orbicie, podobnie jak siła grawitacyjna utrzymuje satelitę na orbicie wokół Ziemi. Zasada działania tych sił jest podobna - utrzymują one ciała w ruchu krążącym wokół innego ciała.
W obu przypadkach, zarówno w atomie wodoru, jak i w przypadku satelity, energia całkowita systemu (suma energii kinetycznej i potencjalnej) pozostaje stała. To oznacza, że jeśli energia kinetyczna rośnie (na przykład w wyniku zwiększenia prędkości), to energia potencjalna musi spadać (na przykład w wyniku zwiększenia odległości od jądra atomowego lub Ziemi).
Wynika stąd matematyczna zależność między energią kinetyczną a potencjalną, którą można wyrazić za pomocą odpowiednich wzorów. W przypadku atomu wodoru jest to wzór 
To podobieństwo wynika z tego, że oba przypadki są przykładami układów dynamicznych, w których energia kinetyczna i potencjalna są ze sobą ściśle powiązane. To dlatego ta zależność między nimi zachodzi.