Najpierw powinno się wartość natężenia pola między okładkami kondensatora. Dzięki temu, że wiemy, że jest ono jednorodne, można skorzystać z zależności:

Podstawiając odpowiednio za różnicę potencjałów tę między okładkami, a za s odległość między nimi otrzymuje się:
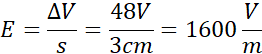
Aby znaleźć odległość między punktami X i Y wystarczy skorzystać z tego, że pole jest jednorodne (tzn. wszędzie takie samo natężenie), a więc potencjał rośnie liniowo, wraz z odległością z tego powodu można zapisać równość:

Praca, jaką musi wykonać pole to:
![]()

W rozwiązaniu założono, że pole pomiędzy okładkami kondensatora jest jednorodne (tzn. jego natężenie jest takie samo w każdym punkcie). Jest to własność pola między okładkami kondensatora, jeśli odległość między nimi jest dużo mniejsza niż ich rozmiary. Można ten fakt przyjąć „na wiarę”. Ambitniejsi uczniowie chcący dowiedzieć się, dlaczego tak jest, mogą zapoznać się z prawem Gaussa, a następnie samemu sobie to wyprowadzić.