W tym zadaniu musisz udowodnić, iż promienie orbit elektronowych w modelu atomu Bohra wyrażają się poprzez ![]()
Zgodnie z klasycznym postulatem Bohra, siła utrzymująca elektron na zwartej orbicie to siła elektrostatyczna:
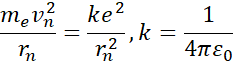
Rozpisując stałą elektrostatyczną i mnożąc przez ![]()
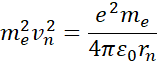
Wykorzystując pierwszy postulat Bohra (postulat o kwantyzacji orbitalnego krętu), orbitalny moment pędu elektronu jest skwantowany:
![]()
Klasycznie wektor momentu pędu (kręt) wyraża się jako:
![]()
Jako, iż w modelu atomu Bohra wektor wodzący jest cały czas prostopadły do wektora pędu, to:
![]()
Wynika stąd formuła na skwantowany moment pędu:
![]()
Dzieląc przez ![]()
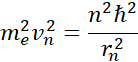
Porównujemy ze sobą prawe strony, wyprowadzone w ramach obu postulatów:

Mnożymy przez ![]()
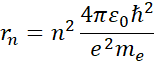
Ostatecznie rozpisujemy ![]()
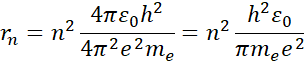
Wyjaśnienie:
W dowodzie wykorzystaj klasyczny postulat Bohra:
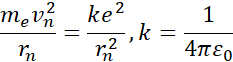
Następnie przekształć go do postaci ![]()
![]()
Przekształć ten wzór do postaci ![]()
![]()


Zadanie 8.
146Zadanie 13.
147Zadanie 14.
147Zadanie 16.
148Zadanie 4.
155Zadanie 13.
156Zadanie 14.
156Zadanie 17.
157Zadanie 1.
162Zadanie 5.
163Zadanie 20.
167Zadanie 21.
168Zadanie 2.
174Zadanie 3.
175Zadanie 5.
175Zadanie 10.
176Zadanie 22.
178Zadanie 2.
181Zadanie 6.
181Zadanie 1.
186Zadanie 3.
187Zadanie 11.
189Zadanie 13.
189Zadanie 17.
190Zadanie 1.
194Zadanie 2.
194Zadanie 3.
195
