W tym zadaniu wyznacz długość i szerokość prostokątnego boiska tak, aby jego powierzchnia była jak największa. Weź pod uwagę, że mamy do dyspozycji farbę wystarczającą do namalowania 60 metrów linii, potrzebnej do wyznaczenia boiska. W obliczeniach nie uwzględniaj szerokości namalowanej linii.

Obwód boiska:
![]()
![]()
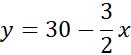
Pole boiska:
![]()
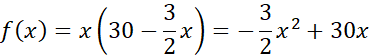
Dziedzina:
![]()
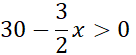
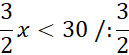
![]()
D = (0, 20)
Aby powierzchnie była największa, należy zobaczyć dla jakiego x funkcja f(x) przyjmuje wartość największą, a przyjmuje ją w wierzchołku (a < 0):
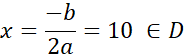
Wtedy:
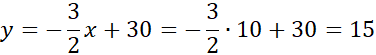
Odp.: Boisko będzie miało największą powierzchnię, jeśli jego wymiary będą wynosiły 10 m x 15 m.

Aby rozwiązać to zadanie rozpocznij od zdefiniowania funkcji opisującej pole boiska. Z treści zadania wiesz, że obwód boiska ma wynosić 60 m. Korzystając z tej informacji możesz wyznaczyć y i zapisać funkcję jako funkcje jednej zmiennej. Współczynnik a < 0 i funkcja przyjmuje wartość największą w wierzchołku. Wartość ta wyraża największe pole, czyli powierzchnię boiska, a współrzędna x wyznacza długość krótszej z linii wyznaczających to boisko.

Zadanie 1.5.
11Zadanie 1.6.
11Zadanie 1.7.
11Zadanie 1.8.
11Zadanie 1.10.
11Zadanie 1.12.
11Zadanie 1.13.
11Zadanie 2.2.
18Zadanie 2.3.
19Zadanie 2.9.
19Zadanie 3.1.
27Zadanie 3.2.
27Zadanie 3.3.
27Zadanie 3.4.
27Zadanie 3.5.
27Zadanie 3.6.
27Zadanie 3.7.
28Zadanie 3.8.
28Zadanie 3.9.
28Zadanie 3.10.
28Zadanie 3.11.
28Zadanie 3.12.
28Zadanie 3.13.
28Zadanie 3.14.
29Zadanie 3.16.
29Zadanie 4.1.
33Zadanie 4.2.
33Zadanie 4.3.
34Zadanie 4.4.
34Zadanie 4.5.
34Zadanie 4.6.
34Zadanie 4.9.
34Zadanie 4.11.
35Zadanie 4.12.
35Zadanie 5.2.
39Zadanie 5.3.
40Zadanie 5.4.
40Zadanie 5.5.
40Zadanie 5.7.
40Zadanie 5.8.
40Zadanie 6.1.
48Zadanie 6.2.
48Zadanie 6.3.
48Zadanie 6.4.
49Zadanie 6.12.
50Zadanie 6.13.
50Zadanie 6.15.
50Zadanie 23.
55Zadanie 24.
55Zadanie 25.
55Zadanie 26.
56Zadanie 27.
56Zadanie 29.
56Zadanie 30.
56Zadanie 31.
56Zadanie 33.
57Zadanie 46.
58Zadanie 47.
58Zadanie 48.
58Zadanie 50.
58
