W tym zadaniu oblicz dla jakiej liczby zamówień fotograf osiągnie największy zysk i jaką będzie wartość tego zysku wiedząc, że wykonał on zdjęcie klasy składającej się z 33 uczniów i ustalił cenę odbitki w następujący sposób: jeśli nie więcej niż 10 osób zamówi odbitki, cena będzie wynosiła 8 zł za odbitkę, a każde kolejne zamówienie spowoduje obniżkę ceny o 0,10 zł dla każdej osoby zamawiającej. Załóż, że koszt wykonania jednej odbitki wynosi fotografa 1 zł.

33 uczniów: 8zł za zdjęcie, jeśli zamówi je nie więcej niż 10 osób.

Powyżej 10 osób:

- grupa 11 osobowa płaci 7,90 zł za zdjęcie od osoby,

- grupa 12 osobowa płaci 7,80 zł za zdjęcie od osoby itd., czyli o 10 gr mniej.

Jeśli x oznacza liczbę osób o którą zwiększy się 10-osobowa grupa, to:

10 + x – liczba zamówień

8 - 0,1x - cena za zdjęcia dla każdej osoby

Kwota jaką otrzyma fotograf:

$\text{[math]}$

Bo grupa nie może być liczniejsza niż 10 + 23 = 33 osoby.

$\text{[math]}$

Aby sprawdzić przy jakiej ilości osób zysk będzie największy, należy zobaczyć dla jakiego x funkcja f(x) przyjmuje wartość największą, a przyjmuje ją w wierzchołku (a < 0):

$\text{[math]}$

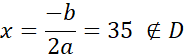
Zysk będzie największy, gdy zdjęcia zamówi 35 osób. Grupa liczy tylko 33 osoby, więc zysk będzie największy gdy wszyscy zamówią zdjęcie.

Wartość zysku:

$\text{[math]}$

Koszt wykonania odbitek:

$\text{[math]}$

Zysk dla fotografa:

$\text{[math]}$

Odp.: Aby zysk fotografa był największy i wynosił 155,1 zł odbitki powinny zamówić 33 osoby.

Możemy opisać cenę zdjęcia za pomocą funkcji kwadratowej postaci:

f(x) = a(x - h)^2 + k,

gdzie x to liczba zamówień, a to współczynnik określający kształt funkcji, h to wartość argumentu dla której funkcja przyjmuje swoją wartość maksymalną, a k to wartość funkcji dla h.

Mając to na uwadze, wyznaczmy wartości h i k.

Dla x = 1, cena wynosi 8 zł, czyli f(1) = 8, co daje:

8 = a(1 - h)^2 + k.

Dla x = 2, cena wynosi 7,90 zł, czyli f(2) = 7,90, co daje:

7,90 = a(2 - h)^2 + k.

Dla x = 3, cena wynosi 7,80 zł, czyli f(3) = 7,80, co daje:

7,80 = a(3 - h)^2 + k.

Rozwiązując ten układ równań, otrzymujemy:

a = -0,05, h = 10, k = 9

W związku z tym, zysk fotografa będzie maksymalny dla x = 10 (wartość argumentu dla której funkcja przyjmuje wartość maksymalną), a wyniesie:

f(10) - 33 = -4 zł

Czyli fotograf straci 4 zł przy sprzedaży 10 zdjęć, ale będzie to dla niego najbardziej opłacalne rozwiązanie, ponieważ zyski z mniejszej liczby zamówień będą jeszcze mniejsze.

Możesz opisać zysk fotografa za pomocą funkcji kwadratowej. Zyskiem będzie cena jednej odbitki pomnożona przez ilość tych odbitek. Ilość odbitek, to 10 + x, ponieważ zamówienie nie może wynosić mniej niż 10 kopii. Jako że otrzymana funkcja ma współczynnik a > 0, to jej wartość największa znajduje się w wierzchołku, którego współrzędne musisz obliczyć. ponieważ mamy serię cen dla grup o różnych rozmiarach, które różnią się od siebie o jeden.