W tym zadaniu przedstaw liczbę 6 jako sumę trzech takich liczb, aby pierwsza była dwa razy większa od drugiej, a suma kwadratów wszystkich liczb była jak najmniejsza.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Suma kwadratów ma wartość najmniejsza w wierzchołku (a > 0):
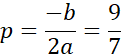
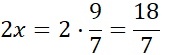
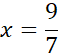
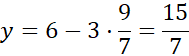

Na podstawie podanych informacji oznacz szukane liczby. Wyznacz wzór funkcji zmiennych, aby opisywał sumę kwadratów tych liczb. Następnie przekształć funkcję tak, aby występowała w niej tylko jedna zmienna. Szukane liczby mają mieć jak najmniejszą sumę kwadratów, dlatego powinieneś znaleźć argument, dla którego funkcja przyjmuje wartość najmniejszą. Otrzymana funkcja jednej zmiennej ma współczynnik a > 0, więc jej wartość najmniejsza znajduję się w wierzchołku. Wyznaczając współrzędne wierzchołka otrzymasz szukaną wartość zmiennej.

Zadanie 1.5.
11Zadanie 1.6.
11Zadanie 1.7.
11Zadanie 1.8.
11Zadanie 1.10.
11Zadanie 1.12.
11Zadanie 1.13.
11Zadanie 2.2.
18Zadanie 2.3.
19Zadanie 2.9.
19Zadanie 3.1.
27Zadanie 3.2.
27Zadanie 3.3.
27Zadanie 3.4.
27Zadanie 3.5.
27Zadanie 3.6.
27Zadanie 3.7.
28Zadanie 3.8.
28Zadanie 3.9.
28Zadanie 3.10.
28Zadanie 3.11.
28Zadanie 3.12.
28Zadanie 3.13.
28Zadanie 3.14.
29Zadanie 3.16.
29Zadanie 4.1.
33Zadanie 4.2.
33Zadanie 4.3.
34Zadanie 4.4.
34Zadanie 4.5.
34Zadanie 4.6.
34Zadanie 4.9.
34Zadanie 4.11.
35Zadanie 4.12.
35Zadanie 5.2.
39Zadanie 5.3.
40Zadanie 5.4.
40Zadanie 5.5.
40Zadanie 5.7.
40Zadanie 5.8.
40Zadanie 6.1.
48Zadanie 6.2.
48Zadanie 6.3.
48Zadanie 6.4.
49Zadanie 6.12.
50Zadanie 6.13.
50Zadanie 6.15.
50Zadanie 23.
55Zadanie 24.
55Zadanie 25.
55Zadanie 26.
56Zadanie 27.
56Zadanie 29.
56Zadanie 30.
56Zadanie 31.
56Zadanie 33.
57Zadanie 46.
58Zadanie 47.
58Zadanie 48.
58Zadanie 50.
58
