W tym zadaniu wyobraź sobie prostokąt T o bokach długości 16 cm i 10 cm, a następnie rozważ nowy prostokąt, o bokach powstałych poprzez dodanie pewnej wartości x do krótszego boku prostokąta T oraz odjecie wartości x od dłuższego boku prostokąta T. Oblicz dla jakiej wartości x pole nowego prostokąta będzie największe.
Rozważmy nowy prostokąt o bokach długości (16 + x) cm i (10 - x) cm. Jego pole wynosi:
![]()
Dziedzina:
![]()
![]()
![]()
![]()
![]()
a < 0, więc funkcja ma wartość największą w wierzchołku:
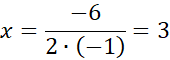
Pole wynosi wtedy:
![]()

Aby rozwiązać to zadania boki prostokąta należy oznaczyć jako 16 + x i 10 – x, jak wynika z opisu. Wyznacz wzór funkcji zmiennej. Pamiętaj o określeniu dziedziny, ponieważ długości boków nie mogą być zerem ani liczbami ujemnymi. Otrzymana funkcja ma a < 0, dlatego funkcja ma wartość największą w wierzchołku. Wyznacz współrzędne wierzchołka i dla otrzymanej współrzędnej x oblicz największą wartość funkcji.

Zadanie 1.5.
11Zadanie 1.6.
11Zadanie 1.7.
11Zadanie 1.8.
11Zadanie 1.10.
11Zadanie 1.12.
11Zadanie 1.13.
11Zadanie 2.2.
18Zadanie 2.3.
19Zadanie 2.9.
19Zadanie 3.1.
27Zadanie 3.2.
27Zadanie 3.3.
27Zadanie 3.4.
27Zadanie 3.5.
27Zadanie 3.6.
27Zadanie 3.7.
28Zadanie 3.8.
28Zadanie 3.9.
28Zadanie 3.10.
28Zadanie 3.11.
28Zadanie 3.12.
28Zadanie 3.13.
28Zadanie 3.14.
29Zadanie 3.16.
29Zadanie 4.1.
33Zadanie 4.2.
33Zadanie 4.3.
34Zadanie 4.4.
34Zadanie 4.5.
34Zadanie 4.6.
34Zadanie 4.9.
34Zadanie 4.11.
35Zadanie 4.12.
35Zadanie 5.2.
39Zadanie 5.3.
40Zadanie 5.4.
40Zadanie 5.5.
40Zadanie 5.7.
40Zadanie 5.8.
40Zadanie 6.1.
48Zadanie 6.2.
48Zadanie 6.3.
48Zadanie 6.4.
49Zadanie 6.12.
50Zadanie 6.13.
50Zadanie 6.15.
50Zadanie 23.
55Zadanie 24.
55Zadanie 25.
55Zadanie 26.
56Zadanie 27.
56Zadanie 29.
56Zadanie 30.
56Zadanie 31.
56Zadanie 33.
57Zadanie 46.
58Zadanie 47.
58Zadanie 48.
58Zadanie 50.
58
