W tym zadaniu oblicz jaka jest najmniejsza możliwa wartość iloczynu dwóch liczb rzeczywistych należących do przedziału (−40, 40) i różniących się od siebie o 12.
![]()
![]()
![]()
Funkcja ma wartość najmniejsza w wierzchołku (a > 0):
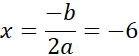
i wtedy:
![]()
Najmniejszy iloczyn:
![]()

Aby rozwiązać to zadanie oznacz szukane liczby jako np. x i x + 12 – są to liczby różniące się o 12. Wyznacz wzór funkcji zmiennych, aby opisywał iloczyn tych liczb. Następnie przekształć funkcję tak, aby występowała w niej tylko jedna zmienna. Współczynnik a > 0, więc funkcja ma najmniejszą wartość, czyli najmniejszy iloczyn w wierzchołku. Wyznacz współrzędne wierzchołka. Współrzędna x jest jedną z szukanych liczb. Oblicz drugą liczbę i ich iloczyn.

Zadanie 1.5.
11Zadanie 1.6.
11Zadanie 1.7.
11Zadanie 1.8.
11Zadanie 1.10.
11Zadanie 1.12.
11Zadanie 1.13.
11Zadanie 2.2.
18Zadanie 2.3.
19Zadanie 2.9.
19Zadanie 3.1.
27Zadanie 3.2.
27Zadanie 3.3.
27Zadanie 3.4.
27Zadanie 3.5.
27Zadanie 3.6.
27Zadanie 3.7.
28Zadanie 3.8.
28Zadanie 3.9.
28Zadanie 3.10.
28Zadanie 3.11.
28Zadanie 3.12.
28Zadanie 3.13.
28Zadanie 3.14.
29Zadanie 3.16.
29Zadanie 4.1.
33Zadanie 4.2.
33Zadanie 4.3.
34Zadanie 4.4.
34Zadanie 4.5.
34Zadanie 4.6.
34Zadanie 4.9.
34Zadanie 4.11.
35Zadanie 4.12.
35Zadanie 5.2.
39Zadanie 5.3.
40Zadanie 5.4.
40Zadanie 5.5.
40Zadanie 5.7.
40Zadanie 5.8.
40Zadanie 6.1.
48Zadanie 6.2.
48Zadanie 6.3.
48Zadanie 6.4.
49Zadanie 6.12.
50Zadanie 6.13.
50Zadanie 6.15.
50Zadanie 23.
55Zadanie 24.
55Zadanie 25.
55Zadanie 26.
56Zadanie 27.
56Zadanie 29.
56Zadanie 30.
56Zadanie 31.
56Zadanie 33.
57Zadanie 46.
58Zadanie 47.
58Zadanie 48.
58Zadanie 50.
58
