Twoim zadaniem w podpunkcie b jest obliczenie zmiany długości fali de Broglie'a cząstki alfa po przejściu przez pole elektrostatyczne.
![]()
![]()
Z rysunku odczytujemy także, że
![]() oraz
oraz
![]()
![]() - ładunek cząstki α, gdzie
- ładunek cząstki α, gdzie
![]() - ładunek elementarny (
- ładunek elementarny (
![]() )
)
![]() - masa cząstki α, gdzie
- masa cząstki α, gdzie
![]() - masa protonu (
- masa protonu (
![]() )
)
Założenie: Cząstka alfa wylatuje z kondensatora i nie uderza w jego dolną
Wchodząc w pole elektryczne cząstka ma prędkość:
![]()
Ważne: na cząstkę w polu działa pole elektryczne. Dzięki niemu cząstka odchyli się w polu.
Uwzględniając obie składowe prędkości (prostopadłą i równoległą):
![]()
Gdzie:
![]()
![]()
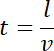
Podstawiając wartości:
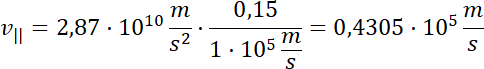
Ostateczna prędkość:
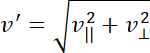
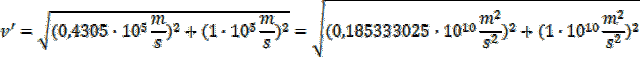
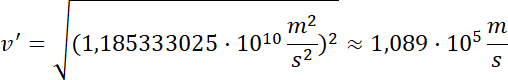
Długość fali de Broglie'a:
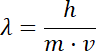
Przed przejściem przez pole elektryczne:
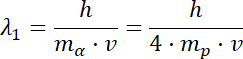
Po przejściu:
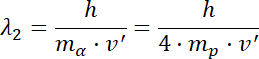
Zmiana długości fali:
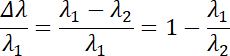
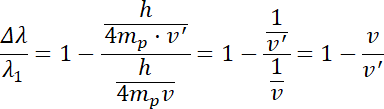
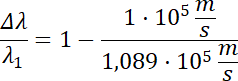
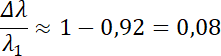
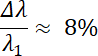

Należy obliczyć wypadkową prędkość cząstki po opuszczeniu kondensatora, łącząc jej prędkość początkową z prędkością wynikającą z przyspieszenia oraz (za pomocą wzoru
![]() ) - długość fali de Broglie'a przed i po przejściu przez pole.
) - długość fali de Broglie'a przed i po przejściu przez pole.

Zadanie 1.5
28Zadanie 1.17
30Zadanie 1.19
31Pytanie 1.26
32Zadanie 1.28
32Zadanie 3.2
35Zadanie 3.3
35Zadanie 3.4
36Zadanie 3.8
36Zadanie 3.11
37Zadanie 3.12
37Zadanie 3.14
38Zadanie 3.15
39Zadanie 4.2
39Zadanie 4.5
40Zadanie 5.6
41Zadanie 5.7
41Zadanie 5.8
42Pytanie 6.1
43Pytanie 6.4
44Zadanie 6.7
45Zadanie 6.8
45Zadanie 6.10
45Zadanie 6.11
46Zadanie 6.15
47Zadanie 6.16
47Zadanie 6.17
47Zadanie 6.18
47Zadanie 6.19
48Zadanie 6.20
48Zadanie 7.3
48Zadanie 7.5
49Zadanie 7.6
50Zadanie 7.7
50Zadanie 8.2
52Zadanie 8.4
53Zadanie 8.9
53Zadanie 8.10
53Zadanie 8.11
53Zadanie 8.14
54Zadanie 8.16
54Zadanie 8.18
54Zadanie 8.22*
55Zadanie 9.7
58Zadanie 10.6
62Zadanie 10.10
62Zadanie 10.11
62
