W tym zadaniu musisz obliczyć wpływ wzrostu temperatury ciała doskonale czarnego na energię emitowaną przez to ciało.
![]() - temperatura ciała doskonale czarnego
- temperatura ciała doskonale czarnego
![]()
![]() - energia promieniowania elektromagnetycznego emitowana przez ciało
- energia promieniowania elektromagnetycznego emitowana przez ciało
![]() - jednostka czasu
- jednostka czasu
![]() - powierzchnia ciała
- powierzchnia ciała
Energia
![]() w jednostce czasu t jest wprost proporcjonalna do czwartej potęgi jego temperatury bezwzględnej
w jednostce czasu t jest wprost proporcjonalna do czwartej potęgi jego temperatury bezwzględnej
![]() . Możemy to zapisać jako:
. Możemy to zapisać jako:
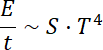
Zatem:
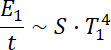
Po zwiększeniu temperatury ciała:
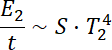
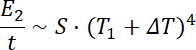
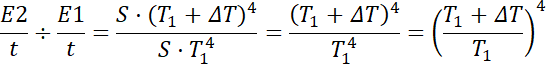
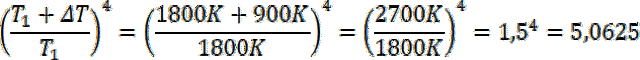

W drugim kroku, aby obliczyć zmianę długości fali, użyj prawa przesunięcia Wiena. Pomoże Ci to ustalić, jak zmieniła się długość fali, przy której występuje maksymalne natężenie promieniowania. Całkowita energia emitowana przez to ciało w jednostce czasu wzrośnie bowiem pięciokrotnie.

Zadanie 1.5
28Zadanie 1.17
30Zadanie 1.19
31Pytanie 1.26
32Zadanie 1.28
32Zadanie 3.2
35Zadanie 3.3
35Zadanie 3.4
36Zadanie 3.8
36Zadanie 3.11
37Zadanie 3.12
37Zadanie 3.14
38Zadanie 3.15
39Zadanie 4.2
39Zadanie 4.5
40Zadanie 5.6
41Zadanie 5.7
41Zadanie 5.8
42Pytanie 6.1
43Pytanie 6.4
44Zadanie 6.7
45Zadanie 6.8
45Zadanie 6.10
45Zadanie 6.11
46Zadanie 6.15
47Zadanie 6.16
47Zadanie 6.17
47Zadanie 6.18
47Zadanie 6.19
48Zadanie 6.20
48Zadanie 7.3
48Zadanie 7.5
49Zadanie 7.6
50Zadanie 7.7
50Zadanie 8.2
52Zadanie 8.4
53Zadanie 8.9
53Zadanie 8.10
53Zadanie 8.11
53Zadanie 8.14
54Zadanie 8.16
54Zadanie 8.18
54Zadanie 8.22*
55Zadanie 9.7
58Zadanie 10.6
62Zadanie 10.10
62Zadanie 10.11
62
