Fizyka. Klasa 4. Zakres rozszerzony. Zbiór zadań - rozwiązania i odpowiedzi

Zbiór zadań, Wydawnictwo: WSiP

Zadanie 10.7 - strona 62

W tym zadaniu musisz obliczyć napięcie, które przyspieszyło cząstkę alfa ze stanu spoczynku na podstawie długości fali, która jej odpowiada. Masz również podane informacje o masie i ładunku cząstki alfa.

$\text{[math]}$

Praca pola elektrycznego:

$\text{[math]}$

Wzór na energię kinetyczną cząsteczki alfa:

$\text{[math]}$

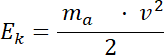
Co daje:

$\text{[math]}$

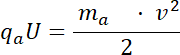
Wzór na długość fali materii:

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

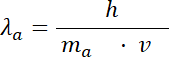
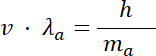
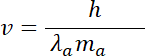
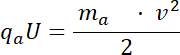
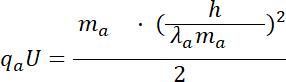
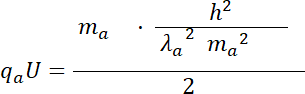
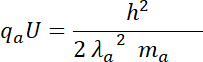
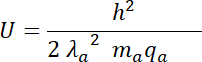
Podstawiamy masę i ładunek cząsteczki alfa:

$\text{[math]}$

$\text{[math]}$

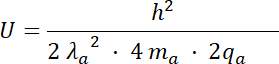
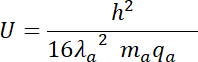
Wykonujemy obliczenia:

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

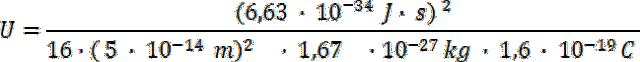
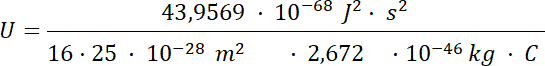
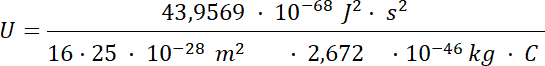
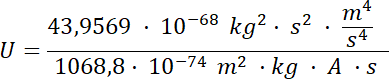
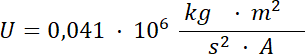
W pierwszym kroku skorzystaj z wzoru de Broglie'a, aby obliczyć pęd cząstki na podstawie jej długości fali. Następnie przekształć pęd w energię kinetyczną cząstki, używając wzoru na energię kinetyczną. W ostatnim kroku skorzystaj z równości energii kinetycznej i pracy wykonanej na cząstkę przez napięcie, aby znaleźć szukane napięcie. Twoim wynikiem jest napięcie, które przyspieszyło cząstkę alfa ze stanu spoczynku.

Zadanie 3., strona 21, Fizyka. Klasa 7. Podręcznik - rozwiązania i odpowiedzi

Zadanie 1., strona 54, Fizyka. Klasa 1. Podręcznik. Zakres podstawowy – rozwiązania i odpowiedzi

Pytanie 13., strona 155, Fizyka. Fizyka z plusem. Klasa 7. Podręcznik - rozwiązania i odpowiedzi

Zadanie 1., strona 19, Świat fizyki. Klasa 8. Podręcznik - rozwiązania i odpowiedzi

Zadanie 2.6., strona 16, Świat fizyki. Klasa 7. Zbiór zadań - rozwiązania i odpowiedzi

Ćwiczenie 7., strona 89, Świat fizyki. Klasa 7. Zeszyt ćwiczeń - rozwiązania i odpowiedzi

Zadanie 5.6.16., strona 207, Zrozumieć fizykę. Klasa 1. Zakres rozszerzony. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 1, strona 167, To jest fizyka. Klasa 7. Podręcznik - rozwiązania i odpowiedzi

Ćwiczenie 1., strona 60, Fizyka. Klasa 8. Zeszyt ćwiczeń - rozwiązania i odpowiedzi

Zadanie 3., strona 172, Fizyka. Fizyka z plusem. Klasa 7. Podręcznik - rozwiązania i odpowiedzi

27

27

27

27

Zadanie 1.5

28

28

28

28

28

28

28

29

29

30

30

30

30

30

Zadanie 1.17

30

30

30

31

Zadanie 1.19

31

31

31

31

31

31

31

31

32

Pytanie 1.26

32

32

32

32

Zadanie 1.28

32

32

32

33

34

34

34

34

35

Zadanie 3.2

35

35

35

35

Zadanie 3.3

35

35

35

35

Zadanie 3.4

36

36

36

36

36

36

Zadanie 3.8

36

36

36

36

36

37

37

Zadanie 3.11

37

37

37

Zadanie 3.12

37

37

37

37

37

37

37

38

Zadanie 3.14

38

38

38

Zadanie 3.15

39

39

39

39

Zadanie 4.2

39

39

39

39

39

Zadanie 4.5

40

40

40

40

40

40

40

41

Zadanie 5.6

41

41

41

Zadanie 5.7

41

41

41

41

41

Zadanie 5.8

42

42

42

42

43

43

Pytanie 6.1

43

43

43

43

44

Pytanie 6.4

44

44

44

44

44

Zadanie 6.7

45

45

45

Zadanie 6.8

45

45

45

45

Zadanie 6.10

45

45

45

45

45

Zadanie 6.11

46

46

46

46

46

46

Zadanie 6.15

47

47

47

47

Zadanie 6.16

47

47

47

Zadanie 6.17

47

47

47

Zadanie 6.18

47

47

47

Zadanie 6.19

48

48

48

48

48

Zadanie 6.20

48

48

48

48

48

Zadanie 7.3

48

48

48

48

49

Zadanie 7.5

49

49

49

49

Zadanie 7.6

50

50

50

Zadanie 7.7

50

50

50

50

50

51

51

51

52

Zadanie 8.2

52

52

52

52

53

Zadanie 8.4

53

53

53

53

53

53

53

Zadanie 8.9

53

53

53

Zadanie 8.10

53

53

53

Zadanie 8.11

53

53

53

54

54

Zadanie 8.14

54

54

54

54

Zadanie 8.16

54

54

54

54

Zadanie 8.18

54

54

54

54

55

55

Zadanie 8.22*

55

55

55

55

56

56

56

56

57

57

Zadanie 9.7

58

58

58

58

58

59

59

59

59

59

59

60

60

60

60

60

60

61

61

61

61

61

62

Zadanie 10.6

62

62

62

62

62

62

62

Zadanie 10.10

62

62

62

Zadanie 10.11

62

62

62

63

63

63

Pełny spis treści