W drugim kroku musisz dowiedzieć się, jak duży fragment ciała musiałby się ochłodzić, aby moc końcowa była taka sama jak moc początkowa.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Chcemy, by:
![]()
![]()
![]()
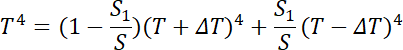
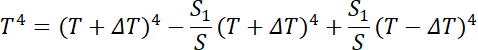
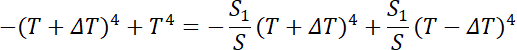
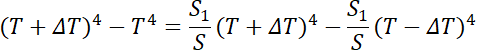
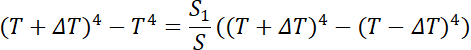
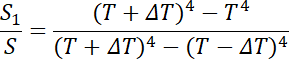
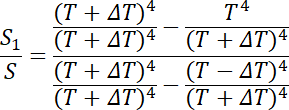
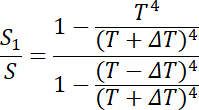
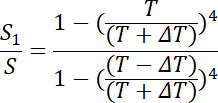
Podstawiamy:
![]() i
i
![]() :
:
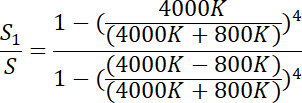
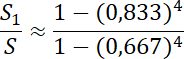
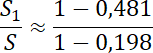
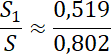
![]()
Więc
![]()

W części b) analizujemy sytuację, w której powierzchnia ciała zostaje podzielona na dwa fragmenty o różnych temperaturach. Twoim zadaniem jest ustalenie, jaka powinna być proporcja tych powierzchni, aby całościowa moc promieniowania ciała nie uległa zmianie.
Aby to osiągnąć, ustaw równanie opisujące moc promieniowania ciała w tej nowej sytuacji i przyrównaj ją do początkowej mocy
![]() . Rozwiązując to równanie względem
. Rozwiązując to równanie względem
![]() uzyskasz proporcję powierzchni ciała, która musi mieć niższą temperaturę, aby moc promieniowania ciała pozostała taka sama.
uzyskasz proporcję powierzchni ciała, która musi mieć niższą temperaturę, aby moc promieniowania ciała pozostała taka sama.

Zadanie 1.5
28Zadanie 1.17
30Zadanie 1.19
31Pytanie 1.26
32Zadanie 1.28
32Zadanie 3.2
35Zadanie 3.3
35Zadanie 3.4
36Zadanie 3.8
36Zadanie 3.11
37Zadanie 3.12
37Zadanie 3.14
38Zadanie 3.15
39Zadanie 4.2
39Zadanie 4.5
40Zadanie 5.6
41Zadanie 5.7
41Zadanie 5.8
42Pytanie 6.1
43Pytanie 6.4
44Zadanie 6.7
45Zadanie 6.8
45Zadanie 6.10
45Zadanie 6.11
46Zadanie 6.15
47Zadanie 6.16
47Zadanie 6.17
47Zadanie 6.18
47Zadanie 6.19
48Zadanie 6.20
48Zadanie 7.3
48Zadanie 7.5
49Zadanie 7.6
50Zadanie 7.7
50Zadanie 8.2
52Zadanie 8.4
53Zadanie 8.9
53Zadanie 8.10
53Zadanie 8.11
53Zadanie 8.14
54Zadanie 8.16
54Zadanie 8.18
54Zadanie 8.22*
55Zadanie 9.7
58Zadanie 10.6
62Zadanie 10.10
62Zadanie 10.11
62
