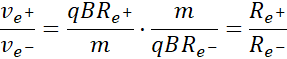![]()
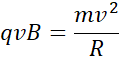
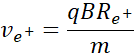
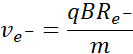
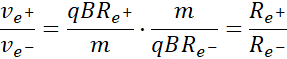
Z treści zadania wiemy, że:
![]()
Zatem stosunek prędkości pozytonu i elektronu wynosi:
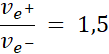

W ruchu po okręgu w polu magnetycznym zakładam, że rolę siły dośrodkowej (w przypadku cząstki) przejmuje siła Lorentza, wszak ona wpływa na zakrzywienie toru ruchu takiej cząstki.
![]()
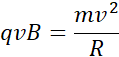
Przekształcając powyższe równanie i dostosowując wynik pod dwie cząstki, które mnie interesują, czyli elektron i pozyton, otrzymuję:
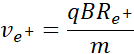
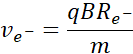
Licząc stosunek powyższych prędkości, otrzymuję: