W tym zadaniu musisz zbudować z 8 sześcianów podanych wymiarach różne prostopadłościany, a następnie obliczyć ich powierzchnie.
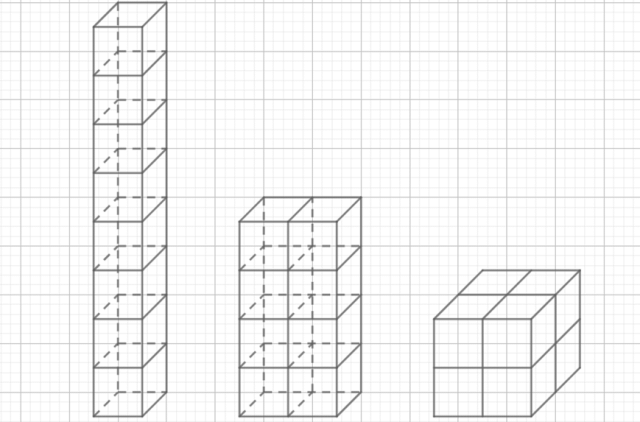
1)
P = 3 cm · 3 cm · 2 + 4 · 3 cm · 24 cm = 18 cm2 + 288 cm2 = 306 cm2
2)
P = 2 · 3 cm · 6 cm + 2 · 3 cm · 12 cm + 2 · 6 cm · 12 cm = 36 cm2 + 72 cm2 + 144 cm2 = 252 cm2
3)
P = 6 · 6 cm · 6 cm = 216 cm2

Na początek zastanówmy się, ile kostek może znaleźć się w podstawie prostopadłościanu, oczywiście można umieścić tam tylko jeden sześcian, wtedy wysokość jest równa wysokości 8 kostek, innym sposobem jest utworzenie podstawy z dwóch kostek, które dadzą prostokąt, położenie pozostałych sześcianów na nich, da wysokość równą wysokości 4 kostek, na koniec można także utworzyć w podstawie kwadrat, wykorzystując do tego cztery sześciany, wysokość takiej bryły to dwie kostki. Wiemy, że krawędź jednego sześcianu to 3 cm, czyli wymiary brył poznamy, mnożąc przez 3 cm, liczbę kostek tworzącą daną krawędź. Pole powierzchni zaś otrzymasz, licząc pola każdego z prostokątów (boki leżące naprzeciwko siebie są identyczne, więc możesz zastąpić dodawanie, mnożeniem), a następnie dodając do siebie te wyniki.

Zadanie 2
265Zadanie 3
265Zadanie 5
265Zadanie 6
266Zadanie 8
266Zadanie 9
266Zadanie 10
266Zadanie 11
266Zadanie 12
267Zadanie 18
267Zadanie 30
270Zadanie wprowadzające 1.
271Zadanie wprowadzające 2.
272Zadanie 1
272Zadanie 2
272Zadanie 6
273Zadanie 7
273Zadanie 10
273Zadanie 11
274Zadanie 12
274Zadanie 13
274Zadanie 17
275Zadanie 18
275Zadanie 27
276Zadanie 3
277Zadanie 4
277Zadanie 5
277Zadanie 6
278Zadanie 8
278Zadanie 9
278Zadanie 11
279Zadanie 12
279Zadanie 13
279Zadanie 14
280Zadanie 15
280Zadanie 17
280Zadanie 20
280Zadanie 22
281Zadanie 26
282Zadanie 1
283Zadanie 6
284Zadanie 9
284Zadanie 10
285Zadanie 11
285Zadanie 12
285Zadanie 13
286Zadanie 14
286Zadanie 22
287Zadanie 25
287
