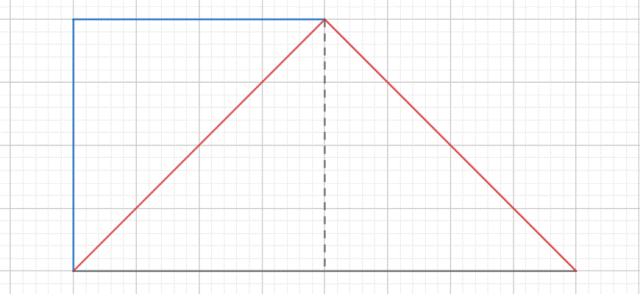
W tym zadaniu musisz naszkicować sobie sytuację przedstawioną w treści, znaleźć wymiary trapezu i ocenić, które zdanie poprawnie opisuje jego powierzchnię.
I) Zadnie jest prawdziwe.
Pole trapezu jest 3 razy większe od pola mniejszego trójkąta.
II) Zdanie jest fałszywe.

W trapezie prostokątnym jedno z ramion styka się z podstawami pod kątem 90 stopni – to ramię będzie także jedną z przyprostokątnych mniejszego trójkąta. Jest on równoramienny, więc krótsza podstawa trapezu też jest jego ramieniem, o tej samej długości. Wiemy, że kąty przy podstawie mają po 45 stopni, więc podstawą trójkąta będzie przekątna łącząca kąt rozwarty trapezu z kątem prostym przy dłuższej podstawie. Teraz dorysujmy drugi, większy trójkąt, jego ramieniem jest narysowana wcześniej przekątna, więc drugie ramię trapezu ma taką samą długość. Tutaj także, pomiędzy podstawą (która jest też dłuższą podstawą trapezu) a ramionami znajdują się 45 stopnie. W następnym kroku musimy zauważyć pewną rzecz: wysokość większego trapezu, padająca na jego przeciwprostokątną, podzieli go na dwa identyczne trójkąty prostokątne, które mają takie same wymiary, co trójkąt, od którego zaczęliśmy rysowanie. Skoro trapez można podzielić na trzy takie same trójkąty, to jest on trzy razy większy od jednego takiego trójkąta.

Zadanie 2
265Zadanie 3
265Zadanie 5
265Zadanie 6
266Zadanie 8
266Zadanie 9
266Zadanie 10
266Zadanie 11
266Zadanie 12
267Zadanie 18
267Zadanie 30
270Zadanie wprowadzające 1.
271Zadanie wprowadzające 2.
272Zadanie 1
272Zadanie 2
272Zadanie 6
273Zadanie 7
273Zadanie 10
273Zadanie 11
274Zadanie 12
274Zadanie 13
274Zadanie 17
275Zadanie 18
275Zadanie 27
276Zadanie 3
277Zadanie 4
277Zadanie 5
277Zadanie 6
278Zadanie 8
278Zadanie 9
278Zadanie 11
279Zadanie 12
279Zadanie 13
279Zadanie 14
280Zadanie 15
280Zadanie 17
280Zadanie 20
280Zadanie 22
281Zadanie 26
282Zadanie 1
283Zadanie 6
284Zadanie 9
284Zadanie 10
285Zadanie 11
285Zadanie 12
285Zadanie 13
286Zadanie 14
286Zadanie 22
287Zadanie 25
287
