W tym zadaniu musisz zapisać wyrażenie, które posłuży do obliczenia wieku chłopców, a następnie ocenić, czy ich wiek można zapisać jako liczby naturalne.
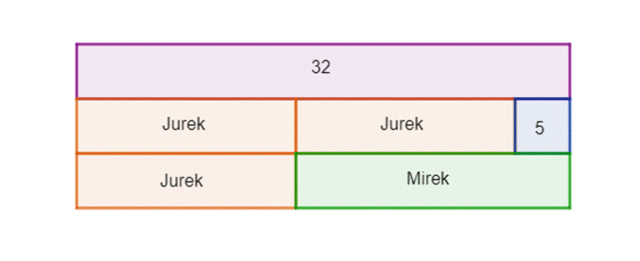
Jurek + 5 = Mirek
Mirek + Jurek = Jurek + Jurek + 5 = 32
Jurek + Jurek = 32 – 5 = 27
Jurek = 27 : 2
Odpowiedź: (B.) Nie, ponieważ (1.) (32 – 5) : 2 nie jest liczbą naturalną.

Możesz posłużyć się rysunkiem. Wiemy, że suma wieku Jurka i Mirka to 32 lata, a Mirek jest o 5 lat starszy, więc jego wiek można zapisać jako wiek Jurka powiększony o 5. W ten sposób dowiadujemy się, że suma podwojonego wieku Jurka i liczby 5 jest równa 32. Po pomniejszeniu obu stron o 5 dowiadujemy się, że podwojony wiek Jurka to 27 lat. Ta liczba nie jest podzielna przez 2, czyli wynik nie jest liczbą naturalną.

Zadanie 2
265Zadanie 3
265Zadanie 5
265Zadanie 6
266Zadanie 8
266Zadanie 9
266Zadanie 10
266Zadanie 11
266Zadanie 12
267Zadanie 18
267Zadanie 30
270Zadanie wprowadzające 1.
271Zadanie wprowadzające 2.
272Zadanie 1
272Zadanie 2
272Zadanie 6
273Zadanie 7
273Zadanie 10
273Zadanie 11
274Zadanie 12
274Zadanie 13
274Zadanie 17
275Zadanie 18
275Zadanie 27
276Zadanie 3
277Zadanie 4
277Zadanie 5
277Zadanie 6
278Zadanie 8
278Zadanie 9
278Zadanie 11
279Zadanie 12
279Zadanie 13
279Zadanie 14
280Zadanie 15
280Zadanie 17
280Zadanie 20
280Zadanie 22
281Zadanie 26
282Zadanie 1
283Zadanie 6
284Zadanie 9
284Zadanie 10
285Zadanie 11
285Zadanie 12
285Zadanie 13
286Zadanie 14
286Zadanie 22
287Zadanie 25
287
