W tym zadaniu musisz zbudować z 12 sześcianów podanych wymiarach różne prostopadłościany, a następnie obliczyć ich powierzchnie.
1)
P = 2 · 2 cm · 2 cm + 4 · 2 cm · 24 cm = 8 cm2 + 192 cm2 = 200 cm2
2)
P = 2 · 2 cm · 4 cm + 2 · 2 cm · 12 cm + 2 · 4 cm · 12 cm = 16 cm2 + 48 cm2 + 96 cm2 = 160 cm2
3)
P = 2 · 4 cm · 4 cm + 4 · 4 cm · 6 cm = 32 cm2 + 96 cm2 = 128 cm2
4)
P = 2 · 2 cm · 6 cm + 2 · 2 cm · 8 cm + 2 · 6 cm · 8 cm = 24 cm2 + 32 cm2 + 96 cm2 = 152 cm2
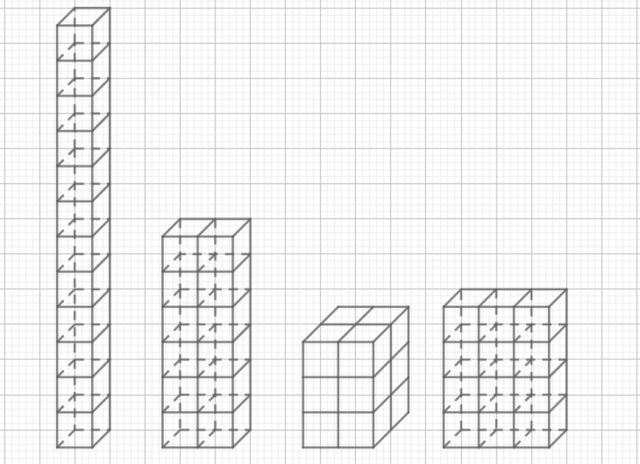

Na początek zastanówmy się, jakie wymiary może mieć prostopadłościan składający się z 12 kostek. Są 4 możliwości: 1 x 1 x 12, 2 x 1 x 6, 2 x 2 x 3 oraz 3 x 1 x 4 (za każdym razem iloczyn wymiarów musi dać 12). Wiemy, że jedna kostka ma 2 cm długości, więc wymiary brył w cm, poznasz, mnożąc długość jednej kostki przez ilość sześcianów tworzących daną krawędź prostopadłościanu. Pole powierzchni bryły otrzymasz, dodając do siebie pola wszystkich jej sześciu prostokątnych ścian (pamiętaj, ściany leżące naprzeciwko siebie są takie same, więc ułatw sobie liczenie, mnożąc pole jednej z nich przez 2).

Zadanie 2
265Zadanie 3
265Zadanie 5
265Zadanie 6
266Zadanie 8
266Zadanie 9
266Zadanie 10
266Zadanie 11
266Zadanie 12
267Zadanie 18
267Zadanie 30
270Zadanie wprowadzające 1.
271Zadanie wprowadzające 2.
272Zadanie 1
272Zadanie 2
272Zadanie 6
273Zadanie 7
273Zadanie 10
273Zadanie 11
274Zadanie 12
274Zadanie 13
274Zadanie 17
275Zadanie 18
275Zadanie 27
276Zadanie 3
277Zadanie 4
277Zadanie 5
277Zadanie 6
278Zadanie 8
278Zadanie 9
278Zadanie 11
279Zadanie 12
279Zadanie 13
279Zadanie 14
280Zadanie 15
280Zadanie 17
280Zadanie 20
280Zadanie 22
281Zadanie 26
282Zadanie 1
283Zadanie 6
284Zadanie 9
284Zadanie 10
285Zadanie 11
285Zadanie 12
285Zadanie 13
286Zadanie 14
286Zadanie 22
287Zadanie 25
287
