W tym zadaniu musisz narysować koło i umieścić na nim odcinki, które utworzą średnicę oraz promień, a następnie połączyć ze sobą jeden z końców średnicy i promienia oraz ocenić, jaki element koła w ten sposób powstał.
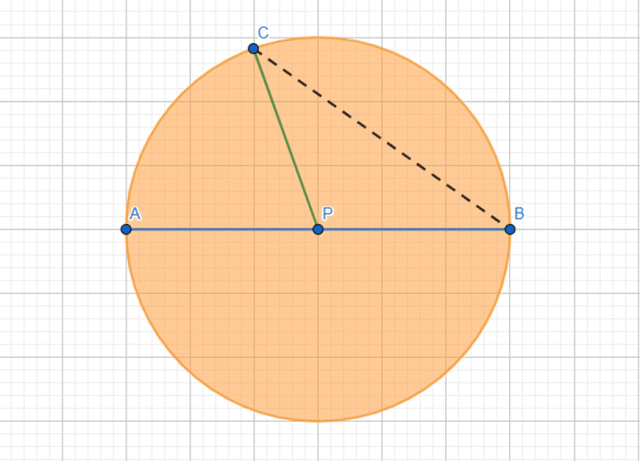
Odpowiedź: Odcinek BC jest cięciwą tego koła, nie jest on średnicą.

Zaznacz w zeszycie punkt P i wbij w jego miejsce cyrkiel, którego nóżki są rozłożone na odległość 3 cm. Zatocz okrąg, my potrzebujemy koła, więc musisz jeszcze zamalować jego wnętrze. Teraz zastanówmy się, gdzie muszą znaleźć się podane punkty. Aby odcinek AB był średnią, musi on przechodzić przez środek koła, czyli punkt P, co oznacza, że punkt A oraz punkt B muszą znaleźć się po dwóch stronach okręgu (koniecznie muszą się znaleźć na obręczy koła, w innym przypadku nie będą jego średnicą), w linii prostej z punktem P. Z punktem C jest łatwiej, jego odległość od punktu P musi być równa promieniowi, a więc punkt C może znaleźć się w dowolnym miejscu na okręgu (gdy znajdzie się wewnątrz okręgu, jego odległość od środka będzie mniejsza od promienia). Teraz możesz połączyć ze sobą punkt B oraz C, zauważ, odcinek nie przechodzi przez środek koła, a więc nie jest to jego średnia. Pamiętaj, każdy odcinek łączący dwa punkty na okręgu, to cięciwa.

Zadanie 2
265Zadanie 3
265Zadanie 5
265Zadanie 6
266Zadanie 8
266Zadanie 9
266Zadanie 10
266Zadanie 11
266Zadanie 12
267Zadanie 18
267Zadanie 30
270Zadanie wprowadzające 1.
271Zadanie wprowadzające 2.
272Zadanie 1
272Zadanie 2
272Zadanie 6
273Zadanie 7
273Zadanie 10
273Zadanie 11
274Zadanie 12
274Zadanie 13
274Zadanie 17
275Zadanie 18
275Zadanie 27
276Zadanie 3
277Zadanie 4
277Zadanie 5
277Zadanie 6
278Zadanie 8
278Zadanie 9
278Zadanie 11
279Zadanie 12
279Zadanie 13
279Zadanie 14
280Zadanie 15
280Zadanie 17
280Zadanie 20
280Zadanie 22
281Zadanie 26
282Zadanie 1
283Zadanie 6
284Zadanie 9
284Zadanie 10
285Zadanie 11
285Zadanie 12
285Zadanie 13
286Zadanie 14
286Zadanie 22
287Zadanie 25
287
