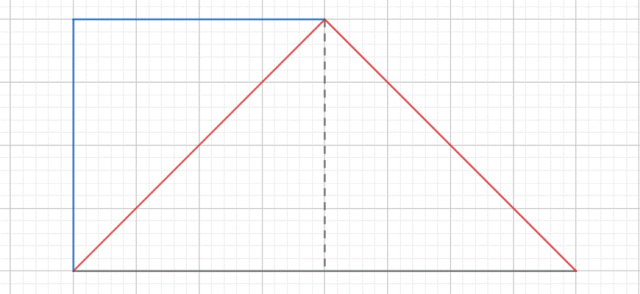
W tym zadaniu musisz naszkicować sobie sytuację przedstawioną w treści, znaleźć wymiary trapezu i podać długość odcinka, który pada prostopadle na najdłuższy bok największego trójkąta.
![]()
a – przyprostokątna mniejszego trójkąta
![]()
![]()
a = h
h – wysokość większego trójkąta
Odpowiedź: C. 4 cm

Skorzystajmy z rysunku pomocniczego wykonanego do podpunktu a. Po dorysowaniu wysokości w większym trójkącie (wychodzi z wierzchołka prostego i pada na środek najdłuższego boku), widzimy, że ma ona taką samą długość, co przyprostokątna mniejszego trójkąta (obie wysokości są także wysokościami tego samego trapezu, czyli muszą być takie same, niezależnie, w którym miejscu są zaznaczone). Musimy więc podać długość ramienia mniejszego trójkąta. Wiemy, że pole powierzchni mniejszego trójkąta to 8 cm2, i możemy je porównać ze wzorem na pole trójkąta prostokątnego (połowa iloczynu długości przyprostokątnych). Najpierw mnożymy obie strony przez 2, co daje nam równość: a2 = 16 cm2, możemy łatwo odgadnąć, że a = 4 cm (bo 4 · 4 = 16).

Zadanie 2
265Zadanie 3
265Zadanie 5
265Zadanie 6
266Zadanie 8
266Zadanie 9
266Zadanie 10
266Zadanie 11
266Zadanie 12
267Zadanie 18
267Zadanie 30
270Zadanie wprowadzające 1.
271Zadanie wprowadzające 2.
272Zadanie 1
272Zadanie 2
272Zadanie 6
273Zadanie 7
273Zadanie 10
273Zadanie 11
274Zadanie 12
274Zadanie 13
274Zadanie 17
275Zadanie 18
275Zadanie 27
276Zadanie 3
277Zadanie 4
277Zadanie 5
277Zadanie 6
278Zadanie 8
278Zadanie 9
278Zadanie 11
279Zadanie 12
279Zadanie 13
279Zadanie 14
280Zadanie 15
280Zadanie 17
280Zadanie 20
280Zadanie 22
281Zadanie 26
282Zadanie 1
283Zadanie 6
284Zadanie 9
284Zadanie 10
285Zadanie 11
285Zadanie 12
285Zadanie 13
286Zadanie 14
286Zadanie 22
287Zadanie 25
287
