W tym zadaniu musisz wykonać rysunek pomocniczy do sytuacji przedstawionej w treści, zapisać odpowiednie równanie pomiędzy obwodami trójkąta i rombu, oraz podać obwód czworokąta.
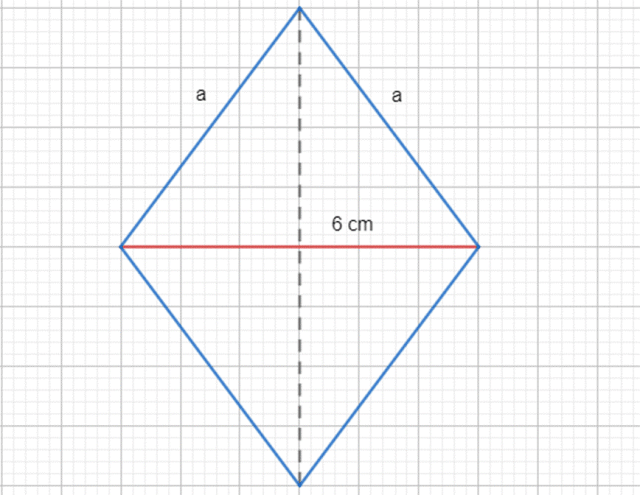
Obwód trójkąta = 2a + 6
Obwód rombu = 4a
4a = 2a + 6 + 14 = 2a + 20
2a = 20
a = 10
Obw = 4a = 4 · 10 = 40
Odpowiedź: Obwód rombu wynosi 40 cm

Jeszcze nie znamy długości boku rombu (wszystkie cztery boki mają taką samą długość), więc zaznaczmy je jako np. literka a. Dorysujmy krótszą przekątną i podpiszmy ją jej długością, czyli 6 centymetrami. Widzimy, że utworzyła ona dwa identyczne trójkąty równoramienne, czyli obwód jednego z nich to a + a + 6 cm. Wiemy, że obwód rombu to 4a, a także, że jest on o 14 cm większy od obwodu trójkąta, a więc do zapisania równości między tymi obwodami, musimy dodać do wyrażenia 2a + 6, jeszcze 14 cm. Teraz widzimy, że 4a = 2a + 2. Tak jak z szalek możemy zdjąć po tle samo, nie martwiąc się o jej przechylenia, tak w tym równaniu możemy odjąć od każdej ze stron po 2a. Teraz widzimy, że 2a = 20, a więc a = 10. Skoro znamy wymiary rombu, pozostaje nam tylko pomnożyć tę długość przez ilość boków – jest to obwód rombu.

Zadanie 2
265Zadanie 3
265Zadanie 5
265Zadanie 6
266Zadanie 8
266Zadanie 9
266Zadanie 10
266Zadanie 11
266Zadanie 12
267Zadanie 18
267Zadanie 30
270Zadanie wprowadzające 1.
271Zadanie wprowadzające 2.
272Zadanie 1
272Zadanie 2
272Zadanie 6
273Zadanie 7
273Zadanie 10
273Zadanie 11
274Zadanie 12
274Zadanie 13
274Zadanie 17
275Zadanie 18
275Zadanie 27
276Zadanie 3
277Zadanie 4
277Zadanie 5
277Zadanie 6
278Zadanie 8
278Zadanie 9
278Zadanie 11
279Zadanie 12
279Zadanie 13
279Zadanie 14
280Zadanie 15
280Zadanie 17
280Zadanie 20
280Zadanie 22
281Zadanie 26
282Zadanie 1
283Zadanie 6
284Zadanie 9
284Zadanie 10
285Zadanie 11
285Zadanie 12
285Zadanie 13
286Zadanie 14
286Zadanie 22
287Zadanie 25
287
