W tym zadaniu musisz zastosować twierdzenie odwrotne do twierdzenia Talesa, aby udowodnić równoległość prostych.
![]()
![]()
![]()
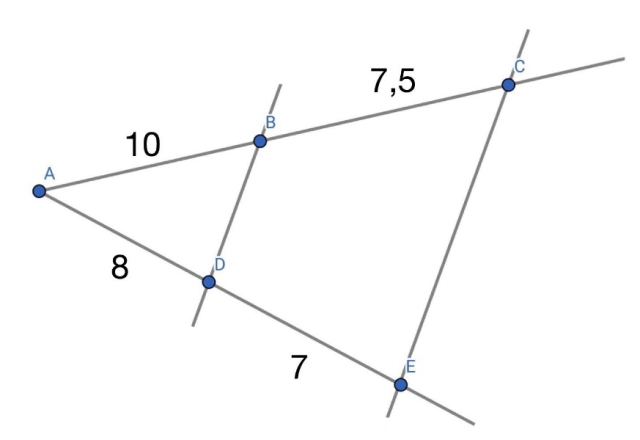
Zatem te proste nie są równoległe.

Twierdzenie odwrotne do twierdzenia Talesa polega na tym, że jeśli kąt przetniemy dwiema prostymi i odpowiednie stosunki odcinków na które te proste podzielą ramiona kątów będą takie same to te proste są równoległe. Zatem jeżeli weźmiemy stosunek długości odcinka od wierzchołka kąta do pierwszej prostej do odcinka między prostymi na tym samym ramieniu kąta i taki sam stosunek na przeciwnym ramieniu wyliczymy je i uzyskamy ten sam wynik to nasze proste są równoległe.

Zadanie 4
206Zadanie 8
206Zadanie 9
207Zadanie 10
207Zadanie 12
207Zadanie 28
208Zadanie 1
209Zadanie 4
209Zadanie 6
210Zadanie 7
210Zadanie 12
210Zadanie 16
211Zadanie 17
211Zadanie 18
211Zadanie 21
212Zadanie 25
212Zadanie 1
213Zadanie 2
213Zadanie 3
213Zadanie 4
213Zadanie 15
215Zadanie 17
215Zadanie 4
216Zadanie 5
216Zadanie 12
217Zadanie 23
218Zadanie 3
219Zadanie 7
220Zadanie 12
220Zadanie 18
221Zadanie 22
222Zadanie 23
222Zadanie 24
222Zadanie 27
222Zadanie 1
223Zadanie 2
223Zadanie 3
223Zadanie 5
223Zadanie 21
225Zadanie 23
225Zadanie 24
225Zadanie 2
226Zadanie 5
226Zadanie 8
226Zadanie 21
228Zadanie 23
228Zadanie 6
229Zadanie 7
229Zadanie 8
229Zadanie 13
230Zadanie 17
230Zadanie 20
231Zadanie 23
231Zadanie 26
232Zadanie 28
232
