W tym zadaniu musisz wykazać podobieństwo trójkątów.
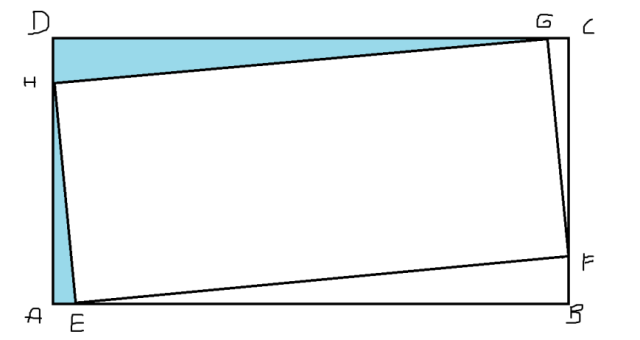
Aby rozwiązać to zadanie należy nazwać kąty, które są wpisane w trójkąty AEH i DGH:
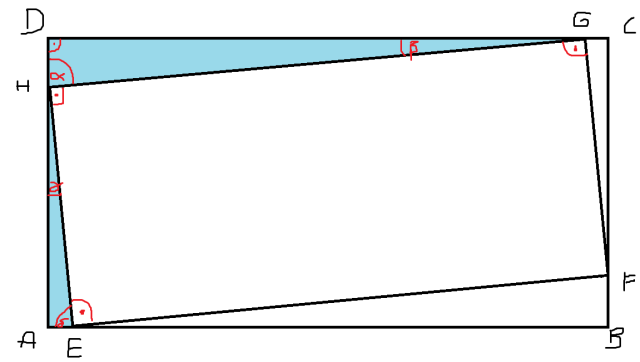
Zakładając, że ∢DHG = α, ∢HGD = β, ∢AHE = γ, ∢AEH = δ możemy ułożyć następujące równania:
![]()
![]()
Z tych dwóch równań wynika, że ![]()
Jeżeli w miejsce γ wstawimy β to otrzymamy następujące równanie:
![]()
Porównując to równanie z równaniem pierwszym otrzymamy zależność
![]()
Kąty tworzące oba trójkąty są równe, zatem na podstawie cechy KKK możemy powiedzieć, że trójkąty HGD i AEH są podobne.

Zacznij od nazwania kątów w rozpatrywanych trójkątach. Następnie, znajdź zależności zachodzące pomiędzy tymi kątami, korzystając z sumy kątów w trójkątach oraz z kątów przyległych.

Zadanie 4
206Zadanie 8
206Zadanie 9
207Zadanie 10
207Zadanie 12
207Zadanie 28
208Zadanie 1
209Zadanie 4
209Zadanie 6
210Zadanie 7
210Zadanie 12
210Zadanie 16
211Zadanie 17
211Zadanie 18
211Zadanie 21
212Zadanie 25
212Zadanie 1
213Zadanie 2
213Zadanie 3
213Zadanie 4
213Zadanie 15
215Zadanie 17
215Zadanie 4
216Zadanie 5
216Zadanie 12
217Zadanie 23
218Zadanie 3
219Zadanie 7
220Zadanie 12
220Zadanie 18
221Zadanie 22
222Zadanie 23
222Zadanie 24
222Zadanie 27
222Zadanie 1
223Zadanie 2
223Zadanie 3
223Zadanie 5
223Zadanie 21
225Zadanie 23
225Zadanie 24
225Zadanie 2
226Zadanie 5
226Zadanie 8
226Zadanie 21
228Zadanie 23
228Zadanie 6
229Zadanie 7
229Zadanie 8
229Zadanie 13
230Zadanie 17
230Zadanie 20
231Zadanie 23
231Zadanie 26
232Zadanie 28
232
