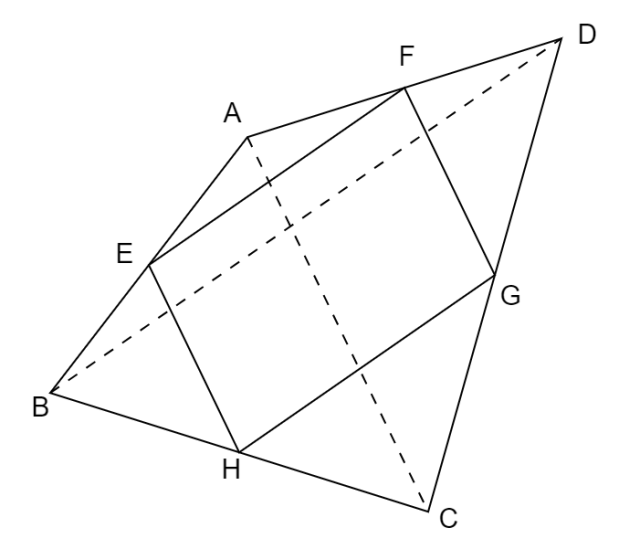
W tym zadaniu musisz wykazać, że czworokąt powstały po połączeniu środków boków dowolnego czworokąta wypukłego to równoległobok o polu równemu połowie pola czworokąta wypukłego.
![]()
![]()
![]()
![]()
![]()
![]()
Z twierdzenie odwrotnego do tw. Talesa, prosta ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Z twierdzenia odwrotnego do tw. Talesa, prosta ![]()
![]()
![]()
W ten sam sposób można pokazać, że ![]()
Czworokąt ![]()
Do wyznaczenia pola, korzystamy z trójkątów podobnych:
Trójkąt ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Zauważmy, że ![]()
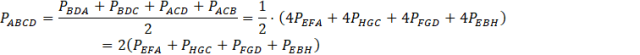
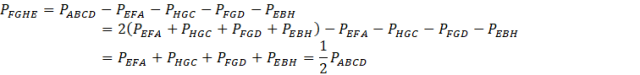

Zauważ, że wierzchołki nowego czworokąta, dzielą boki zewnętrznego czworokąta na pół. Skorzystaj z twierdzenia odwrotnego do tw. Talesa, aby pokazać równoległość boków wewnętrznego czworokąta, co oznacza, że jest on równoległobokiem. Następnie skorzystaj z podobieństwa trójkątów powstałych w czworokącie, aby znaleźć zależność między polem równoległoboku a czworokąta wypukłego.

Zadanie 4
206Zadanie 8
206Zadanie 9
207Zadanie 10
207Zadanie 12
207Zadanie 28
208Zadanie 1
209Zadanie 4
209Zadanie 6
210Zadanie 7
210Zadanie 12
210Zadanie 16
211Zadanie 17
211Zadanie 18
211Zadanie 21
212Zadanie 25
212Zadanie 1
213Zadanie 2
213Zadanie 3
213Zadanie 4
213Zadanie 15
215Zadanie 17
215Zadanie 4
216Zadanie 5
216Zadanie 12
217Zadanie 23
218Zadanie 3
219Zadanie 7
220Zadanie 12
220Zadanie 18
221Zadanie 22
222Zadanie 23
222Zadanie 24
222Zadanie 27
222Zadanie 1
223Zadanie 2
223Zadanie 3
223Zadanie 5
223Zadanie 21
225Zadanie 23
225Zadanie 24
225Zadanie 2
226Zadanie 5
226Zadanie 8
226Zadanie 21
228Zadanie 23
228Zadanie 6
229Zadanie 7
229Zadanie 8
229Zadanie 13
230Zadanie 17
230Zadanie 20
231Zadanie 23
231Zadanie 26
232Zadanie 28
232
