dzielniki wyrazu wolnego: -1, 1, -3, 3
13 + 12 – 5 · 1 + 3 = 0, więc 1 jest pierwiastkiem tego równania
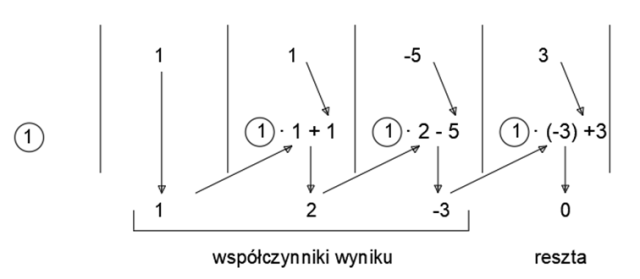
Zatem wielomian x3 + x2 – 5x + 3 jest podzielny przez (x – 1)
x3 + x2 – 5x + 3 = (x – 1)(x2 + 2x – 3)
x3 + x2 – 5x + 3 = 0
(x – 1)(x2 + 2x – 3) = 0
x – 1 = 0 lub x2 + 2x – 3= 0
![]()
![]()
Pierwiastkami tego równania są liczby: -3, 1.

Jeśli wielomian W(x) jest podzielny przez dwumian D(x) = x - a, to W(a) = 0. W tym zadaniu uzupełnij schemat Hornera. Wiedząc, że dany wielomian w(x) jest podzielny przez dwumian (x – a), dając wynik f(x), możesz go zapisać za pomocą w(x) = (x – a) · f(x). Pierwsza linijka schematu Hornera są to współczynniki przy kolejnych wyrazach, natomiast wartość zapisana w kółeczku to wartość a. Po rozwiązaniu schematu Hornera otrzymasz wartość współczynników wielomianu, powstającego wskutek podzielenia wielomianu w(x) przez dwumian (x – a). Aby rozwiązać powyższe równanie, skorzystaj z następujących wzorów: ∆ = b2 – 4ac oraz x1 =
![]() i x2 =
i x2 =
![]() .
.