W(x) = x3 – 4x2 – 5x + 14
a = -2
W(-2) = (-2)3 – 4 · (-2)2 – 5 · (-2) + 14 = 0
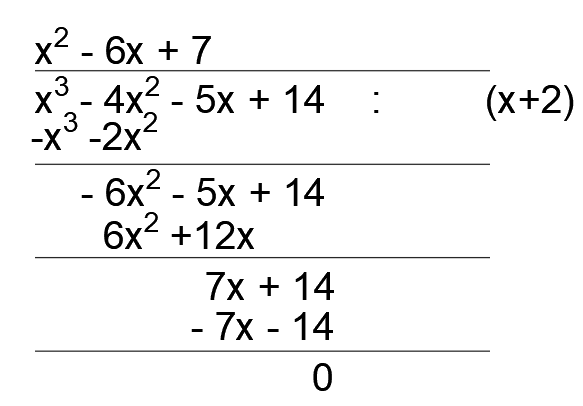
W(x) = (x + 2)(x2 – 6x + 7)
x3 – 4x2 – 5x + 14 = 0
(x + 2)(x2 – 6x + 7) = 0
x + 2 = 0 lub x2 – 6x + 7 = 0
![]()
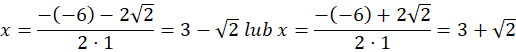
Pozostałymi pierwiastkami tego równania są liczby:
![]()

Jeśli wielomian W(x) jest podzielny przez dwumian D(x) = x – a, gdzie a to dzielniki wyrazu wolnego, to wtedy W(a) = 0, co oznacza, że jeżeli podstawisz za „x”, wartość a to wartość wielomianu będzie równa zeru.