W tym zadaniu znajdź pierwiastek całkowity wielomianu x3 + 3x2 + 3x + 2, a następnie pokaż, że ten wielomian nie ma więcej pierwiastków.
W(-2) = (-2)3 + 3 ∙ (-2)2 + 3 ∙ (-2)+ 2 = 0
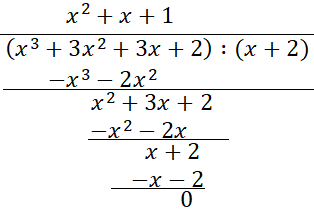
W(x) = (x + 2)(x2 + x + 1)
(x + 2)(x2 + x + 1) = 0
![]()
Jedyne rozwiązanie tego wielomianu to x = -2.

Wyraz wolny równania x3 + 3x2 + 3x + 2 = 0 wynosi 2. Aby ustalić, które liczby całkowite spełniają to równanie, musisz wypisać wszystkie całkowite dzielniki liczby 2 i sprawdzić, czy dla któregoś z nich W(x) = 0.
Całkowite dzielniki liczby 2: 1, -1, 2, -2.
W(-2) = (-2)3 + 3 ∙ (-2)2 + 3 ∙ (-2)+ 2 = 0 ⇒ -2 jest pierwiastkiem tego wielomianu
Podziel wielomian W(x) przez dwumian x + 2.
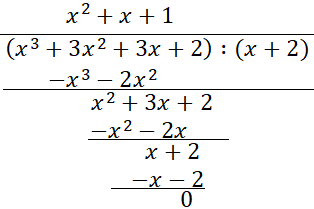
W(x) = (x + 2)(x2 + x + 1)
Przyrównaj wielomian do zera, by znaleźć jego pierwiastki.
(x + 2)(x2 + x + 1) = 0
Zauważ, że drugie wyrażenie to równanie kwadratowe. Rozwiąż je korzystając ze wzoru na deltę:
![]()
Jedyne rozwiązanie tego wielomianu to x = -2.

Ćwiczenie B
11Przykład Uporządkuj wielomian.
11Przykład Oblicz wartość podanego wielomianu dla .
12Zadanie 1
13Zadanie 2
13Zadanie 3
13Zadanie 4
13Zadanie 5
13Zadanie 6
13Zadanie 7
13Zadanie 8
13Zadanie 9
14Zadanie 10
13Zadanie 11
14Zadanie 12
14Zadanie 13
14Zadanie 15
14Ćwiczenie A
15Przykład 1
15Przykład 2
15Przykład 3
15Zadanie 1
18Zadanie 2
18Zadanie 3
18Zadanie 4
18Zadanie 5
19Zadanie 6
19Zadanie 7
19Zadanie 8
19Zadanie 9
19Zadanie 10
19Zadanie 11
19Zadanie 12
20Zadanie 13
20Zadanie 14
20Zadanie 15
20Ćwiczenie A
21Ćwiczenie B
21Przykład 1
22Ćwiczenie C
23Zadanie 1
24Zadanie 2
24Zadanie 3
24Zadanie 4
24Zadanie 5
24Zadanie 6
24Zadanie 7
24Zadanie 8
25Zadanie 9
25Zadanie 10
25Zadanie 11
25Ćwiczenie A
26Zadanie 1
29Zadanie 2
29Zadanie 3
29Zadanie 4
30Zadanie 5
30Zadanie 6
30Zadanie 7
30Zadanie 9
30Zadanie 12
32Zadanie 1
35Zadanie 2
35Zadanie 3
35Zadanie 4
35Zadanie 5
35Zadanie 7
36Ćwiczenie C
38Zadanie 1
40Zadanie 2
40Zadanie 3
40Zadanie 4
41Zadanie 5
41Zadanie 6
41Zadanie 2
42Zadanie 3
42Zadanie 5
42Zadanie 6
42Zadanie 7
42Zadanie 8
42Zadanie 9
42Zadanie 10
42Zadanie 11
42
