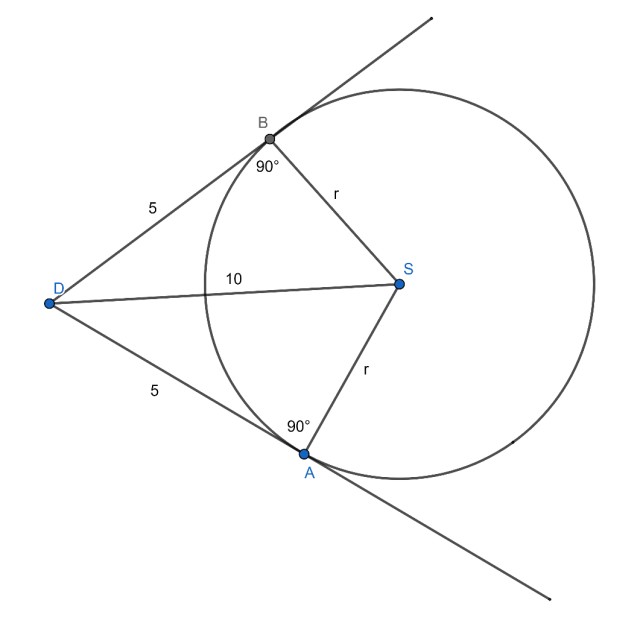
W tym zadaniu oblicz obwód czworokąta o wierzchołkach D, A, S, B, jeżeli wiadomo, że |DS| = 10 i |DA| = 5. Ramiona kąta ADB są styczne do okręgu ośrodku S w punktach A i B.
r2 + 52 = 102
r2 + 25 = 100 / - 25
r2 = 75
![]()
![]()

Z twierdzenia o odcinkach stycznych wiadomo, że |DA| = |DB| = 5. Zauważ, że powstały 2 trójkąty prostokątne o takich samych wymiarach 5, r, 10. Skorzystaj z twierdzenia Pitagorasa a2 + b2 = c2, gdzie a i b to długości przyprostokątnych, a c to przeciwprostokątna trójkąta prostokątnego.
r2 + 52 = 102
r2 + 25 = 100 / - 25
r2 = 75
![]()
Oblicz obwód figury DASB.
![]()

Zadanie 1
135Zadanie 2
135Zadanie 3
135Zadanie 6
135Zadanie 7
136Zadanie 8
136Zadanie 12
136Zadanie 13
137Zadanie 14
137Zadanie 15
137Zadanie 17
137Zadanie 6
141Zadanie 11
142Zadanie B
145Zadanie 1
147Zadanie 2
147Zadanie 7
148Zadanie 8
148Zadanie 11
148Zadanie 13
149Zadanie 15
149Ćwiczenie 1
151Zadanie 1
153Zadanie 2
153Zadanie 3
153Zadanie 10
154Ćwiczenie A
155Ćwiczenie F
157Zadanie 1
158Zadanie 3
158Zadanie 4
158Zadanie 5
158Zadanie 6
158Zadanie 7
158Zadanie 8
158Zadanie 10
159Zadanie 11
159Zadanie 12
159Zadanie 13
159Zadanie 15
160Zadanie 17
160Zadanie 19
160Zadanie 20
160Zadanie 21
161Zadanie 23
161Zadanie 4
162Zadanie 5
162Zadanie 10
162Zadanie 11
162
