W tym zadaniu oblicz miary kątów trójkątów: ostrokątnego, równoramiennego i prostokątnego oraz miary kątów oznaczonych literami.
Przyjmij oznaczenia jak na rysunku.
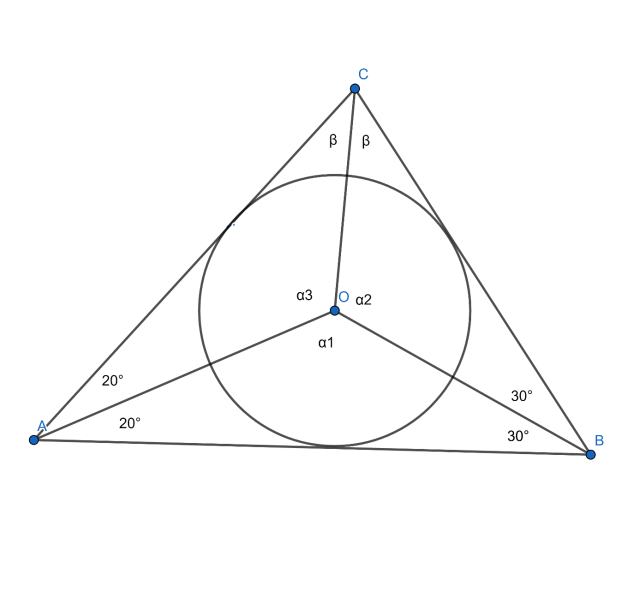
α1 = 180° – 20° – 30° = 130°
180° – 40° – 60° = 80° = 2β / : 2
β = 40°
α2 = 180° – 40° – 30° = 110°
α3 = 180° – 20° – 40° = 120°
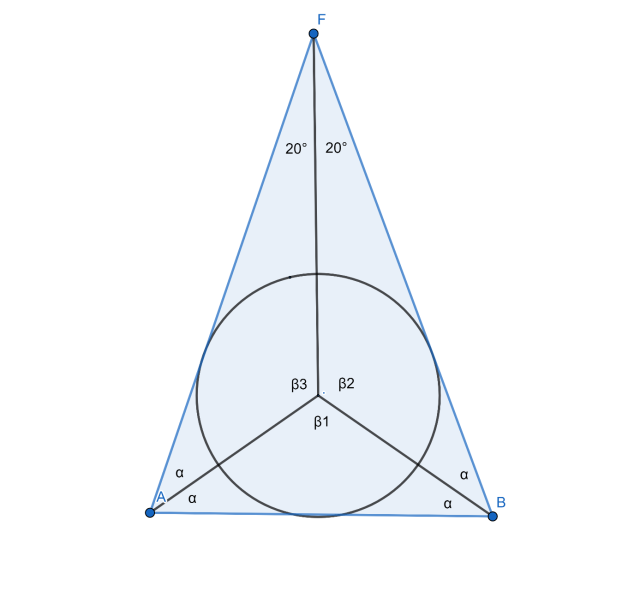
180° – 40 ° = 140°
140° : 2 = 70° ⇒α = 70° : 2 = 35°
β1 = 180° – 35° – 35° = 110°
β2 = β3 = 180° – 35° – 20° = 125°
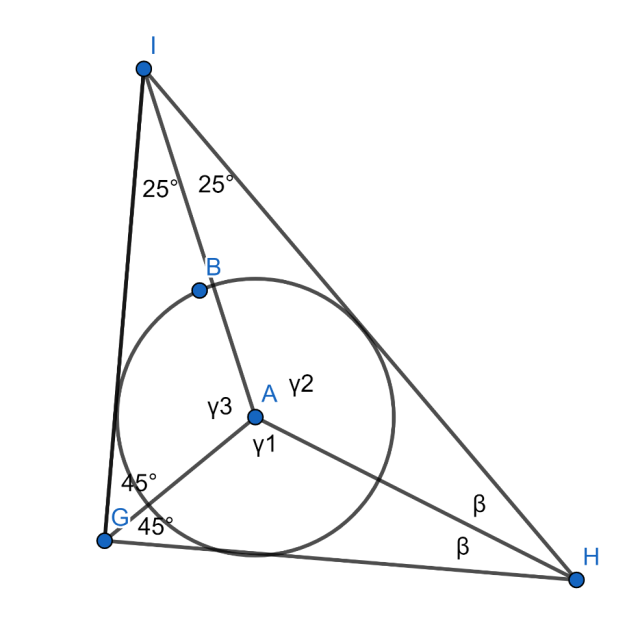
180° – 90° – 50° = 2β
2β = 40° / : 2
β = 20°
γ1 = 180° – 45° – 20° = 115°
γ2 = 180° – 25° – 20° = 135°
γ3 = 180° – 25° – 45° = 110°

Punkt przecięcia dwusiecznych to środek okręgu wpisanego w trójkąt. Skorzystaj z własności, że suma kątów w trójkącie daje 180°.

Zadanie 1
135Zadanie 2
135Zadanie 3
135Zadanie 6
135Zadanie 7
136Zadanie 8
136Zadanie 12
136Zadanie 13
137Zadanie 14
137Zadanie 15
137Zadanie 17
137Zadanie 6
141Zadanie 11
142Zadanie B
145Zadanie 1
147Zadanie 2
147Zadanie 7
148Zadanie 8
148Zadanie 11
148Zadanie 13
149Zadanie 15
149Ćwiczenie 1
151Zadanie 1
153Zadanie 2
153Zadanie 3
153Zadanie 10
154Ćwiczenie A
155Ćwiczenie F
157Zadanie 1
158Zadanie 3
158Zadanie 4
158Zadanie 5
158Zadanie 6
158Zadanie 7
158Zadanie 8
158Zadanie 10
159Zadanie 11
159Zadanie 12
159Zadanie 13
159Zadanie 15
160Zadanie 17
160Zadanie 19
160Zadanie 20
160Zadanie 21
161Zadanie 23
161Zadanie 4
162Zadanie 5
162Zadanie 10
162Zadanie 11
162
