W tym zadaniu oblicz miarę kąta AOB wiedząc, że w trójkąt równoramienny ABC, w którym kąt między ramionami AC i BC ma 100°, wpisano okrąg o środku O.
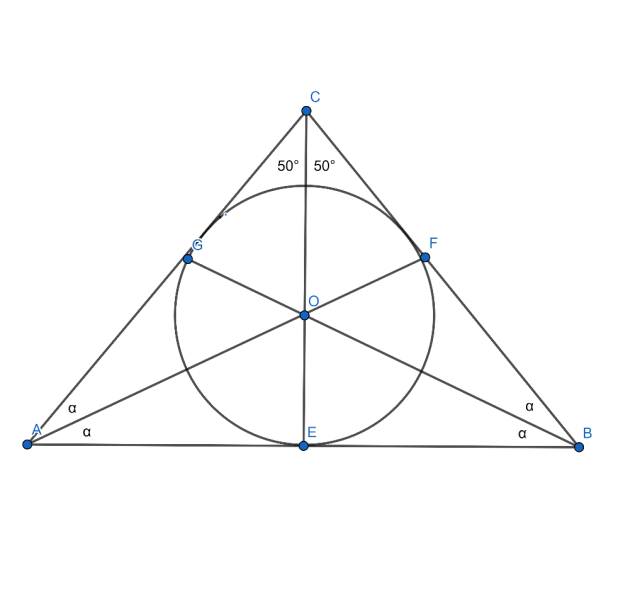
2α + 2α + 100° = 180°
4α + 100° = 180° / - 100°
4α = 80° / : 4
α = 20°
Kąt AOB: 180° – 20° – 20° = 140°.

Skorzystaj z własności, że suma kątów w trójkącie wynosi 180°. W trójkącie równoramiennym kąty przy podstawie są takie same.

Zadanie 1
135Zadanie 2
135Zadanie 3
135Zadanie 6
135Zadanie 7
136Zadanie 8
136Zadanie 12
136Zadanie 13
137Zadanie 14
137Zadanie 15
137Zadanie 17
137Zadanie 6
141Zadanie 11
142Zadanie B
145Zadanie 1
147Zadanie 2
147Zadanie 7
148Zadanie 8
148Zadanie 11
148Zadanie 13
149Zadanie 15
149Ćwiczenie 1
151Zadanie 1
153Zadanie 2
153Zadanie 3
153Zadanie 10
154Ćwiczenie A
155Ćwiczenie F
157Zadanie 1
158Zadanie 3
158Zadanie 4
158Zadanie 5
158Zadanie 6
158Zadanie 7
158Zadanie 8
158Zadanie 10
159Zadanie 11
159Zadanie 12
159Zadanie 13
159Zadanie 15
160Zadanie 17
160Zadanie 19
160Zadanie 20
160Zadanie 21
161Zadanie 23
161Zadanie 4
162Zadanie 5
162Zadanie 10
162Zadanie 11
162
