W tym zadaniu określ, jaki promień ma okrąg opisany na trójkącie równoramiennym o podstawie długości 12 i wysokości opuszczonej na tę podstawę równej 8.
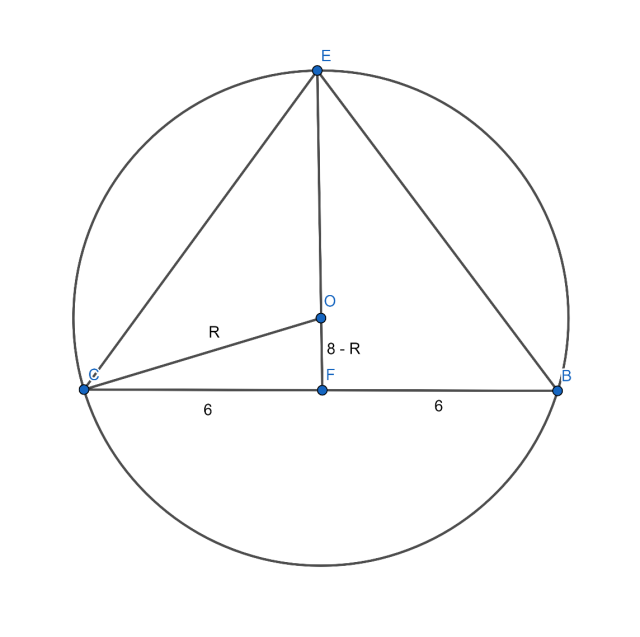
R2 = 62 + (8 - R)2
R2 = 36 + 64 – 16R + R2 / - R2
-16R + 100 = 0 / + 16R
16R = 100 / : 16
R = 6,25

Zauważ, że trójkąt CFO to trójkąt prostokątny. Skorzystaj z twierdzenia Pitagorasa a2 + b2 = c2, gdzie a i b to długości przyprostokątnych, a c to przeciwprostokątna trójkąta prostokątnego.
R2 = 62 + (8 - R)2
Skorzystaj ze wzoru skróconego mnożenia (a - b)2 = a2 - 2ab + b2.
R2 = 36 + 64 – 16R + R2 / - R2
-16R + 100 = 0 / + 16R
16R = 100 / : 16
R = 6,25

Zadanie 1
135Zadanie 2
135Zadanie 3
135Zadanie 6
135Zadanie 7
136Zadanie 8
136Zadanie 12
136Zadanie 13
137Zadanie 14
137Zadanie 15
137Zadanie 17
137Zadanie 6
141Zadanie 11
142Zadanie B
145Zadanie 1
147Zadanie 2
147Zadanie 7
148Zadanie 8
148Zadanie 11
148Zadanie 13
149Zadanie 15
149Ćwiczenie 1
151Zadanie 1
153Zadanie 2
153Zadanie 3
153Zadanie 10
154Ćwiczenie A
155Ćwiczenie F
157Zadanie 1
158Zadanie 3
158Zadanie 4
158Zadanie 5
158Zadanie 6
158Zadanie 7
158Zadanie 8
158Zadanie 10
159Zadanie 11
159Zadanie 12
159Zadanie 13
159Zadanie 15
160Zadanie 17
160Zadanie 19
160Zadanie 20
160Zadanie 21
161Zadanie 23
161Zadanie 4
162Zadanie 5
162Zadanie 10
162Zadanie 11
162
