W tym zadaniu oblicz, jaka jest miara kąta wpisanego w okrąg, opartego na cięciwie o długości równej promieniowi tego okręgu. Uwaga. Zadanie ma dwa rozwiązania
Przypadek 1:
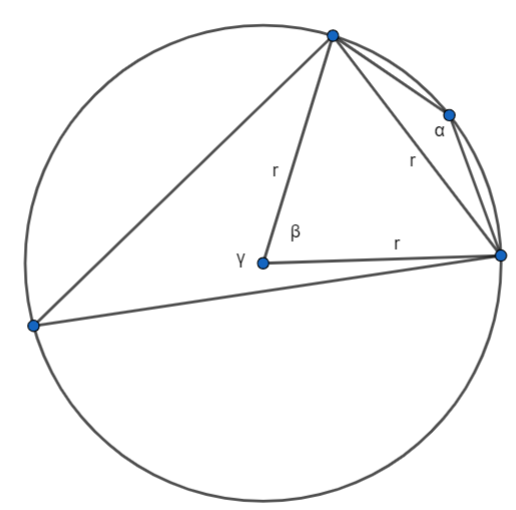
Powstał trójkąt równoboczny o boku r, więc β = 60˚.
α = β : 2 = 60˚ : 2 = 30˚
Przypadek 2:
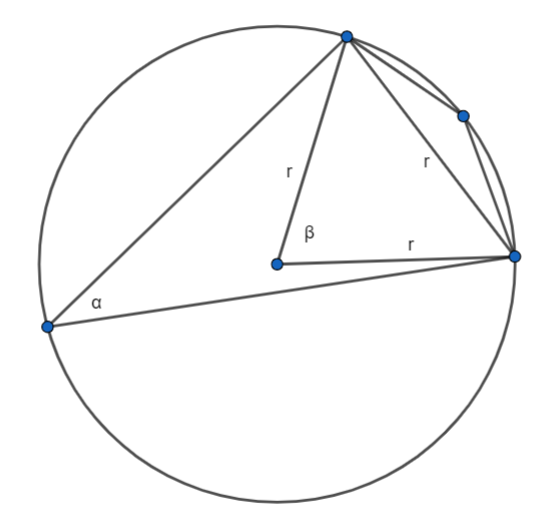
β = 60˚
γ = 360˚ - 60˚ = 300˚
α = 300˚ : 2 = 150˚

Przypadek 1: w trójkącie równobocznym miara każdego kąta wynosi 60˚. Twierdzenie o kątach wpisanych i środkowym opartych na tym samym łuku okręgu mówi, że kąt wpisany ma dwa razy większą miarę niż kąt środkowy oparty na tym samym łuku.
Przypadek 2: skorzystaj z tego samego twierdzenia, co w pierwszym przypadku.

Zadanie 1
135Zadanie 2
135Zadanie 3
135Zadanie 6
135Zadanie 7
136Zadanie 8
136Zadanie 12
136Zadanie 13
137Zadanie 14
137Zadanie 15
137Zadanie 17
137Zadanie 6
141Zadanie 11
142Zadanie B
145Zadanie 1
147Zadanie 2
147Zadanie 7
148Zadanie 8
148Zadanie 11
148Zadanie 13
149Zadanie 15
149Ćwiczenie 1
151Zadanie 1
153Zadanie 2
153Zadanie 3
153Zadanie 10
154Ćwiczenie A
155Ćwiczenie F
157Zadanie 1
158Zadanie 3
158Zadanie 4
158Zadanie 5
158Zadanie 6
158Zadanie 7
158Zadanie 8
158Zadanie 10
159Zadanie 11
159Zadanie 12
159Zadanie 13
159Zadanie 15
160Zadanie 17
160Zadanie 19
160Zadanie 20
160Zadanie 21
161Zadanie 23
161Zadanie 4
162Zadanie 5
162Zadanie 10
162Zadanie 11
162
