W tym zadaniu określ, czy istnieje wielokąt, który ma 30 przekątnych oraz czy istnieje wielokąt, który ma 170 przekątnych.
Sprawdź, czy istnieje wielokąt, który ma 30 przekątnych:
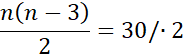
n2 – 3n = 60 / - 60
n2 – 3n – 60 = 0
![]()
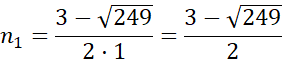
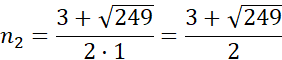
Żadne z rozwiązań nie jest liczbą naturalną, więc nie istnieje wielokąt, który ma 30 przekątnych.
Sprawdź, czy istnieje wielokąt, który ma 170 przekątnych:
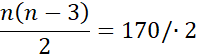
n2 – 3n = 340 / - 340
n2 – 3n – 340 = 0
![]()
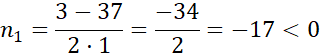
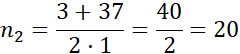
Wielokąt, który ma 170 przekątnych to dwudziestokąt.

Liczba przekątnych w n-kącie wynosi ![]()
Sprawdź, czy istnieje wielokąt, który ma 30 przekątnych:
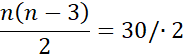
n2 – 3n = 60 / - 60
n2 – 3n – 60 = 0
Wyznacz rozwiązania korzystając ze wzoru na deltę ![]()
![]()
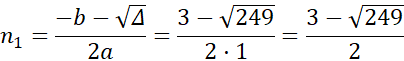
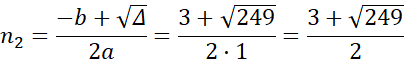
Żadne z rozwiązań nie jest liczbą naturalną, więc nie istnieje wielokąt, który ma 30 przekątnych.
Sprawdź, czy istnieje wielokąt, który ma 170 przekątnych:
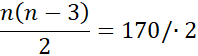
n2 – 3n = 340 / - 340
n2 – 3n – 340 = 0
Wyznacz rozwiązania korzystając ze wzoru na deltę ![]()
![]()
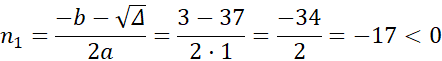
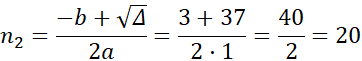
Wielokąt, który ma 170 przekątnych to dwudziestokąt.

Zadanie 1
135Zadanie 2
135Zadanie 3
135Zadanie 6
135Zadanie 7
136Zadanie 8
136Zadanie 12
136Zadanie 13
137Zadanie 14
137Zadanie 15
137Zadanie 17
137Zadanie 6
141Zadanie 11
142Zadanie B
145Zadanie 1
147Zadanie 2
147Zadanie 7
148Zadanie 8
148Zadanie 11
148Zadanie 13
149Zadanie 15
149Ćwiczenie 1
151Zadanie 1
153Zadanie 2
153Zadanie 3
153Zadanie 10
154Ćwiczenie A
155Ćwiczenie F
157Zadanie 1
158Zadanie 3
158Zadanie 4
158Zadanie 5
158Zadanie 6
158Zadanie 7
158Zadanie 8
158Zadanie 10
159Zadanie 11
159Zadanie 12
159Zadanie 13
159Zadanie 15
160Zadanie 17
160Zadanie 19
160Zadanie 20
160Zadanie 21
161Zadanie 23
161Zadanie 4
162Zadanie 5
162Zadanie 10
162Zadanie 11
162
