W tym zadaniu wskaż wzór rekurencyjny ciągu za pomocą jego pięciu początkowych wyrazów:
![]() .
.
![]()
![]()
![]()
![]()
Wynika stąd, że:
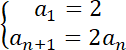
Odpowiedź: Wzór rekurencyjny podanego ciągu to
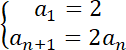 .
.

Rozwiązując to zadanie zauważ zależność, taką, że wyraz następny ciągu, jest dwukrotnością wyrazu poprzedniego. Stosując tą zasadę wyznacz, iż wzór rekurencyjny w tym zadaniu wynosi
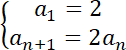 .
.

Zadanie 1.5.
199Zadanie 1.6.
199Zadanie 1.7.
199Zadanie 1.9.
200Zadanie 1.10.
200Zadanie 1.11.
200Zadanie 1.12.
200Zadanie 1.13.
200Zadanie 1.14.
201Zadanie 1.18.
201Zadanie 1.19.
201Zadanie 1.20.
201Zadanie 1.21.
201Zadanie 1.22.
202Zadanie 1.24.
202Zadanie 1.26.
202Zadanie 1.27.
202Zadanie 1.28.
202Zadanie 1.30.
202Zadanie 1.31.
203Zadanie 1.32.
203Zadanie 1.33.
203Zadanie 1.34.
203Zadanie 2.6.
211Zadanie 2.7.
212Zadanie 2.8.
212Zadanie 2.9.
212Zadanie 2.10.
212Zadanie 2.11.
212Zadanie 2.21.
213Zadanie 2.24.
213Zadanie 2.26.
214Zadanie 2.27.
214Zadanie 2.29.
214Zadanie 2.30.
214Zadanie 2.35.
214Zadanie 3.5.
220Zadanie 3.6.
220Zadanie 3.8.
221Zadanie 3.9.
221Zadanie 3.13.
221Zadanie 3.16.
221Zadanie 3.17.
222Zadanie 3.31.
223Zadanie 4.6.
231Zadanie 4.7.
232Zadanie 4.8.
232Zadanie 4.9.
232Zadanie 4.10.
232Zadanie 4.12.
232Zadanie 4.13.
232Zadanie 4.22.
233Zadanie 5.4.
238Zadanie 5.5.
239Zadanie 5.7.
239Zadanie 5.8.
239Zadanie 5.18.
240Zadanie 5.19.
241Zadanie 6.6.
253Zadanie 6.14.
254Zadanie 6.19.
255Zadanie 6.21.
255Zadanie 6.22.
255Zadanie 3.
256Zadanie 37.
261Zadanie 38.
261Zadanie 40.
262Zadanie 41.
262Zadanie 42.
262Zadanie 43.
262Zadanie 47.
262Zadanie 53.
263Zadanie 60.
264Zadanie 73.
265Zadanie 86.
266
