W tym zadaniu udowodnij, że żaden z wyrazów nieskończonego ciągu arytmetycznego o wyrazie ogólnym
![]() nie jest kwadratem liczby naturalnej.
nie jest kwadratem liczby naturalnej.
![]()
![]()
![]()
![]()
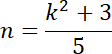
Odpowiedź: Powyższy zapis oznacza, że liczba
![]() jest podzielna przez 5. Wynika stąd, że cyfrą jedności liczby
jest podzielna przez 5. Wynika stąd, że cyfrą jedności liczby
![]() jest 2 albo 7 (bo wówczas
jest 2 albo 7 (bo wówczas
![]() lub
lub
![]() ). W ten sposób dochodzimy do sprzeczności, ponieważ cyfrą jedności kwadratu liczby naturalnej mogą być: 0, 1, 4, 5, 6, 9.
). W ten sposób dochodzimy do sprzeczności, ponieważ cyfrą jedności kwadratu liczby naturalnej mogą być: 0, 1, 4, 5, 6, 9.

Przeprowadź dowód nie wprost. Przypuść, że dla pewnego
![]() wyraz
wyraz
![]() jest kwadratem pewnej liczby naturalnej. Oznacza to, że istnieje takie
jest kwadratem pewnej liczby naturalnej. Oznacza to, że istnieje takie
![]() , że:
, że:
![]()
![]()
![]()
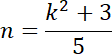
Powyższy zapis oznacza, że liczba
![]() jest podzielna przez 5. Wynika stąd, że cyfrą jedności liczby
jest podzielna przez 5. Wynika stąd, że cyfrą jedności liczby
![]() jest 2 albo 7 (bo wówczas
jest 2 albo 7 (bo wówczas
![]() lub
lub
![]() ). W ten sposób dochodzimy do sprzeczności, ponieważ cyfrą jedności kwadratu liczby naturalnej mogą być: 0, 1, 4, 5, 6, 9.
). W ten sposób dochodzimy do sprzeczności, ponieważ cyfrą jedności kwadratu liczby naturalnej mogą być: 0, 1, 4, 5, 6, 9.

Zadanie 1.5.
199Zadanie 1.6.
199Zadanie 1.7.
199Zadanie 1.9.
200Zadanie 1.10.
200Zadanie 1.11.
200Zadanie 1.12.
200Zadanie 1.13.
200Zadanie 1.14.
201Zadanie 1.18.
201Zadanie 1.19.
201Zadanie 1.20.
201Zadanie 1.21.
201Zadanie 1.22.
202Zadanie 1.24.
202Zadanie 1.26.
202Zadanie 1.27.
202Zadanie 1.28.
202Zadanie 1.30.
202Zadanie 1.31.
203Zadanie 1.32.
203Zadanie 1.33.
203Zadanie 1.34.
203Zadanie 2.6.
211Zadanie 2.7.
212Zadanie 2.8.
212Zadanie 2.9.
212Zadanie 2.10.
212Zadanie 2.11.
212Zadanie 2.21.
213Zadanie 2.24.
213Zadanie 2.26.
214Zadanie 2.27.
214Zadanie 2.29.
214Zadanie 2.30.
214Zadanie 2.35.
214Zadanie 3.5.
220Zadanie 3.6.
220Zadanie 3.8.
221Zadanie 3.9.
221Zadanie 3.13.
221Zadanie 3.16.
221Zadanie 3.17.
222Zadanie 3.31.
223Zadanie 4.6.
231Zadanie 4.7.
232Zadanie 4.8.
232Zadanie 4.9.
232Zadanie 4.10.
232Zadanie 4.12.
232Zadanie 4.13.
232Zadanie 4.22.
233Zadanie 5.4.
238Zadanie 5.5.
239Zadanie 5.7.
239Zadanie 5.8.
239Zadanie 5.18.
240Zadanie 5.19.
241Zadanie 6.6.
253Zadanie 6.14.
254Zadanie 6.19.
255Zadanie 6.21.
255Zadanie 6.22.
255Zadanie 3.
256Zadanie 37.
261Zadanie 38.
261Zadanie 40.
262Zadanie 41.
262Zadanie 42.
262Zadanie 43.
262Zadanie 47.
262Zadanie 53.
263Zadanie 60.
264Zadanie 73.
265Zadanie 86.
266
