W tym zadaniu podaj taką liczbę
![]() , żeby ciąg
, żeby ciąg
![]() był ciągiem arytmetycznym.
był ciągiem arytmetycznym.
![]() dla wszystkich
dla wszystkich
![]() i
i
![]()
![]()
![]()
![]()
![]()
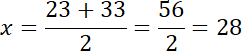
Odpowiedź: Liczba
![]() wynosi 28.
wynosi 28.

Przypomnij sobie, że w ciągu arytmetycznym
![]() zachodzi zależność dla :
zachodzi zależność dla :
![]() dla wszystkich
dla wszystkich
![]() i
i
![]() .
.
W szczególności warunek ten zachodzi pomiędzy trzema sąsiednimi wyrazami. Załóż, że:
![]()
![]()
![]()
Wynika stąd, że:
![]()
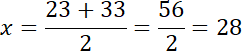

Zadanie 1.5.
199Zadanie 1.6.
199Zadanie 1.7.
199Zadanie 1.9.
200Zadanie 1.10.
200Zadanie 1.11.
200Zadanie 1.12.
200Zadanie 1.13.
200Zadanie 1.14.
201Zadanie 1.18.
201Zadanie 1.19.
201Zadanie 1.20.
201Zadanie 1.21.
201Zadanie 1.22.
202Zadanie 1.24.
202Zadanie 1.26.
202Zadanie 1.27.
202Zadanie 1.28.
202Zadanie 1.30.
202Zadanie 1.31.
203Zadanie 1.32.
203Zadanie 1.33.
203Zadanie 1.34.
203Zadanie 2.6.
211Zadanie 2.7.
212Zadanie 2.8.
212Zadanie 2.9.
212Zadanie 2.10.
212Zadanie 2.11.
212Zadanie 2.21.
213Zadanie 2.24.
213Zadanie 2.26.
214Zadanie 2.27.
214Zadanie 2.29.
214Zadanie 2.30.
214Zadanie 2.35.
214Zadanie 3.5.
220Zadanie 3.6.
220Zadanie 3.8.
221Zadanie 3.9.
221Zadanie 3.13.
221Zadanie 3.16.
221Zadanie 3.17.
222Zadanie 3.31.
223Zadanie 4.6.
231Zadanie 4.7.
232Zadanie 4.8.
232Zadanie 4.9.
232Zadanie 4.10.
232Zadanie 4.12.
232Zadanie 4.13.
232Zadanie 4.22.
233Zadanie 5.4.
238Zadanie 5.5.
239Zadanie 5.7.
239Zadanie 5.8.
239Zadanie 5.18.
240Zadanie 5.19.
241Zadanie 6.6.
253Zadanie 6.14.
254Zadanie 6.19.
255Zadanie 6.21.
255Zadanie 6.22.
255Zadanie 3.
256Zadanie 37.
261Zadanie 38.
261Zadanie 40.
262Zadanie 41.
262Zadanie 42.
262Zadanie 43.
262Zadanie 47.
262Zadanie 53.
263Zadanie 60.
264Zadanie 73.
265Zadanie 86.
266
