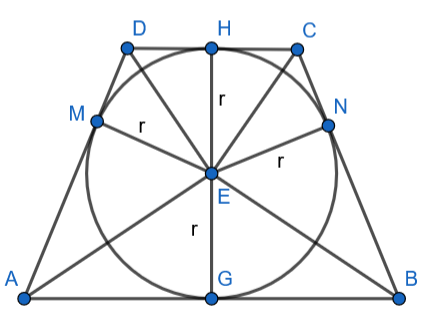
Trójkąty HEC i CEN, NEB i GEB, AEG i AME oraz MDE i DHE są przystające z cechy BKB: są prostokątne, mają wspólną przeciwprostokątną i jedna z przyprostokątnych jest promieniem okręgu. Więc:
Suma miar kątów leżących przy jednym ramieniu trapezu jest równa :Suma miar kątów w trójkącie wynosi :
Oznacza to, że trójkąty AED i BEC są prostokątne. W trójkącie prostokątnym iloczyn stosunku długości odcinków na jakie wysokość podzieliła przeciwprostokątną jest równy jej kwadratowi, więc:
To kończy dowód.
