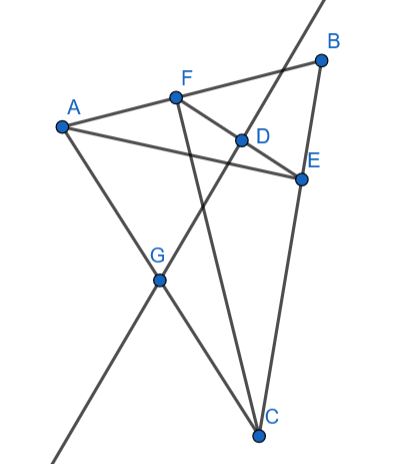
Trójkąty AFC i AEC są prostokątne, więc na czworokącie AFEC można opisać okrąg, którego środek znajduję się w połowie odcinka AC – punkcie G.
Trójkąt GFE jest równoramienny – ramiona mają długość promienia okręgu, więc wysokość trójkąta równoramiennego opadająca na podstawę FE przecina ją w połowie i pod kątem prostym – jest ona jednocześnie symetralną odcinka EF.
To kończy dowód.
